Înainte de a efectua o analiză a răspunsului seismic local, este posibil să se definească un set de noduri monitorizate, la care vor fi returnate rezultatele analizei. Avantajul atribuirii nodurilor monitorizate este o reducere considerabilă a timpului de calcul, deoarece răspunsul seismic local va fi returnat numai cu referire la aceste noduri și nu pentru întregul domeniu. Pentru a selecta un nod monitorizat, în panoul "Instrumente", după selectarea nodului, pur și simplu faceți click pe butonul „Adăugați noduri monitorizate" din bara de sus.

Nodurile monitorizate sunt evidențiate așa cum se arată în figura de mai sus.
Pentru a efectua analiza răspunsului seismic local, este necesar să utilizați butonul „ Analiza răspunsului seismic ” din panoul Analiză și rezultate. Această comandă va avea ca rezultat fereastra prezentată mai jos.
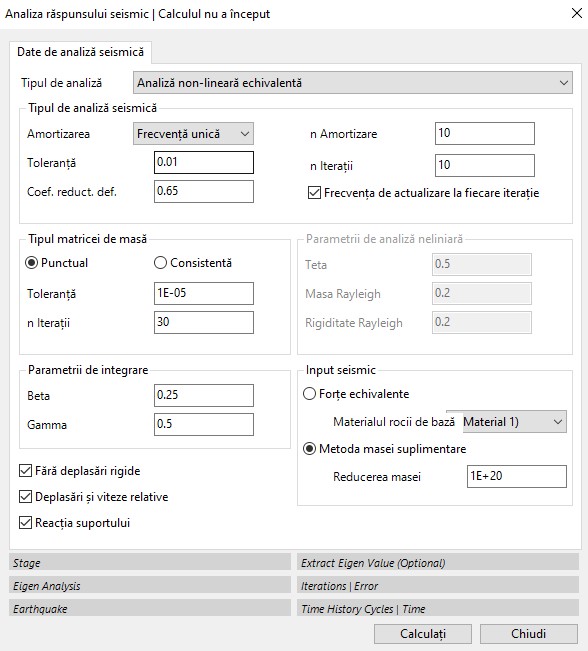
Mai multe opțiuni de analiză pot fi selectate în această fereastră, inclusiv:
a) Fără deplasări rigide
b) deplasări și viteze relative
Opțiunea (a) nu ia în considerare deplasarea rigidă absolută a sistemului în analiza dinamică. În general, această opțiune ar trebui selectată, deoarece deplasările rigide nu conduc la tensiuni suplimentare.
Selectarea opțiunii (b) returnează deplasarea relativă pentru fiecare nod la sfârșitul calculului, altfel deplasarea returnată este deplasarea absolută.
Dati analisi sismica
Software-ul RSL III 2D permite patru tipuri de analiză:
▪Analiza non-lineară echivalentă
▪Analiza liniară cu amortizare variabilă
▪Analiza liniară cu amortizare constantă
▪Analiza dinamică
Tipi di analisi possibili in RSL III 2D
Din punct de vedere teoretic, analiza dinamică pentru un număr finit de noduri se realizează prin rezolvarea unui sistem de ecuații de tipul:
![]()
unde
[M] = matricea masei
[C] = matricea de amortizare
[K] = matricea rigidității
R = vectorul de sarcini cunoscute egal cu [M]agcu accelerograma de intrare ag.
u este vectorul deplasărilor relative.
Sistemul este rezolvat în domeniul timpului în conformitate cu criteriul lui Newmark: constă într-o serie de integrări succesive, pentru fiecare pas Δt, pentru a determina viteza și, prin urmare, deplasarea relativă u. Atunci când se aplică metoda lui Newton, sunt necesari anumiți parametri de integrare (caseta roșie din figura următoare).
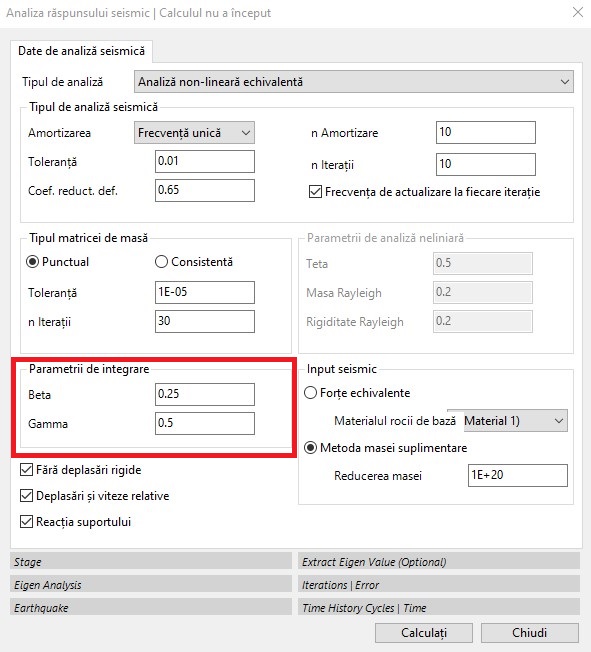
Beta și Gamma sunt doi parametri ai metodei de integrare Newmark care au în general valori de 0,25 și, respectiv, 0,5.
Amortizarea terenului este luată în considerare prin matricea [C]. Pentru fiecare element i în care este împărțit domeniul, Ci este calculat conform criteriului Rayleigh, care este corelat cu masa și rigiditatea:
Ci=α∙Mi+β∙Ki
Unde α și β sunt doi coeficienți numiți, respectiv, masa Rayleigh și rigiditatea Rayleigh, în timp ce Mi și Ki sunt masa și rigiditatea elementului individual. Folosind această formulare, amortizarea λ (sau raportul de amortizare) poate fi făcută dependentă de frecvența circulară în conformitate cu următoarea relație:
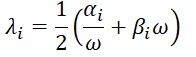
unde α și β pentru al i-lea element sunt calculate după cum urmează:
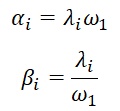
cu ω1 frecvența principală corespunzătoare primului mod de vibrație.
Analiză liniară cu amortizare constantă (caseta roșie din figura de mai jos): software-ul efectuează calculul utilizând matricea de amortizare consistentă a lui Rayleigh cu α și β constante pentru toate nodurile și egale cu valorile indicate în Masa Rayleigh și Rigiditatea Rayleigh.
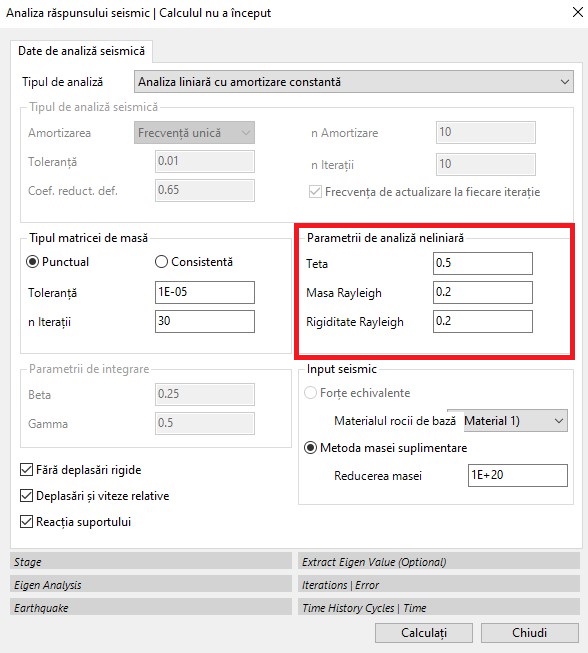
Teta este un parametru de integrare stabilit în general la 0,5
Analiza amortizării variabile liniare: software-ul efectuează calculul folosind parametrii definiți în grila de materiale ca parametri de amortizare.
Analiza echivalentă neliniară (caseta roșie din imaginea următoare)
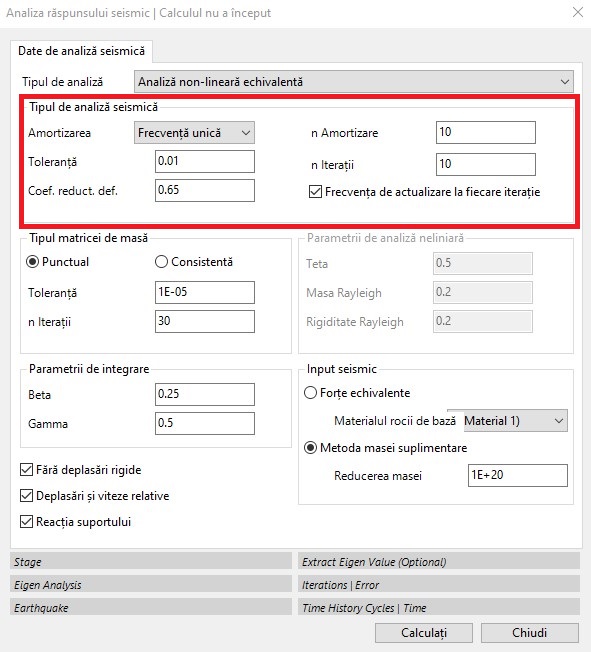
În acest caz, software-ul efectuează o secvență de analize liniare în care parametrii de rigiditate și amortizare sunt actualizați iterativ până când se atinge un factor de convergență. Calculul începe cu valorile inițiale ale G și D introduse în fereastra de materiale și se determină deformarea de forfecare legată de valoarea deplasării u. În fiecare iterație, valorile D și G/Gmax sunt actualizate în funcție de nivelul de deformare efectivă atins, iar calculul se oprește atunci când diferența dintre valorile G și D între o iterație și următoarea este mai mică decât nivelul de toleranță stabilit de utilizator.
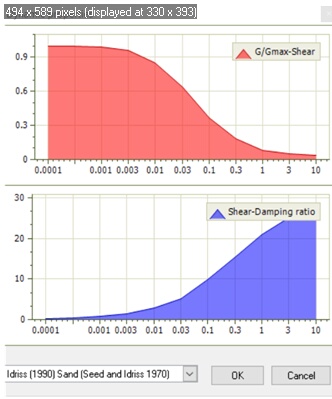
Pentru acest tip de analiză, se poate alege, de asemenea, să se actualizeze frecvența circulară ω la fiecare iterație. Acest lucru implică faptul că calculul coeficienților Rayleigh α și β din matricea de amortizare C sunt actualizați la fiecare iterație pentru fiecare element în funcție de frecvența principală ω1, în cazul frecvenței unice, sau de ω1 și ω2 în cazul frecvenței duble. Pentru fiecare element, în cazul frecvenței duble, expresiile α și β sunt:
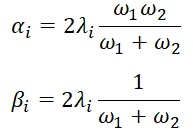
cu ω1 frecvența principală și ω2 = nDamp x ω1 , cu nDamp în general stabilit egal cu 10. Practic, pentru fiecare iterație se calculează deformația de forfecare medie pentru fiecare element și se consultă curba de amortizare pentru a actualiza valoarea corectă a amortizării.
Toleranța definește abaterea dintre valorile G și D, găsite între o iterație și următoarea, care determină sfârșitul calculului iterativ.
Numărul de iterații determină numărul de iterații care urmează să fie efectuate de program: un număr mare de iterații (> 10) duce la o creștere inutilă a timpului de calcul.
Coeff. Red. Def. Acesta este un coeficient care reduce deformarea maximă; valoarea sa este de obicei stabilită la 0,65. Se calculează din următoarea expresie: γeff/γmax = (M-1)/10
Alți parametri ai analizei neliniare echivalente se referă la analiza modală cu elemente finite în care trebuie definită matricea de masă (caseta roșie):
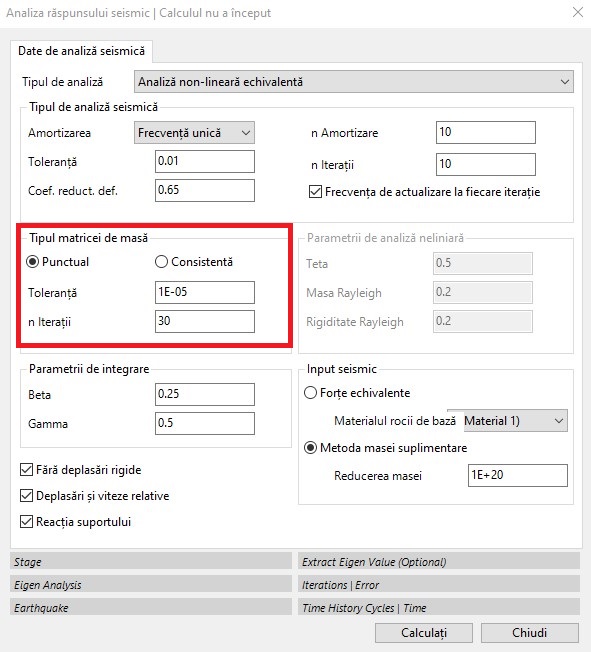
Masa punctuală: masa este considerată a fi concentrată la noduri.
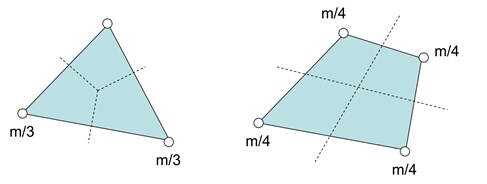
În acest caz, structura matricei de masă este diagonală și prezintă avantaje considerabile în ceea ce privește ocuparea redusă a memoriei și o reducere semnificativă a timpului de calcul. De obicei, această ipoteză nu conduce la erori mari și, prin urmare, este preferabilă.
Masa uniformă: masa este distribuită, iar matricea corespunzătoare este substanțial completă și simetrică. Această ipoteză produce erori mai mici în valoare absolută, dar conduce la o creștere a timpului de calcul.
Parametrii analizei modale: Pentru analiza modală, trebuie setat un factor de toleranță, care determină momentul în care calculul trebuie oprit, și un număr de iterații. Dacă calculul atinge numărul de iterații stabilit, acesta se oprește chiar dacă toleranța dorită nu este atinsă. Analiza modală trebuie efectuată pentru toate nodurile din domeniu, astfel încât nu este efectuată de software atunci când există noduri monitorizate.
Introducere seismică
Atunci când se efectuează calculul RSL III 2D, pot fi alese două metode diferite: Forțe echivalente și Metoda masei adăugate.
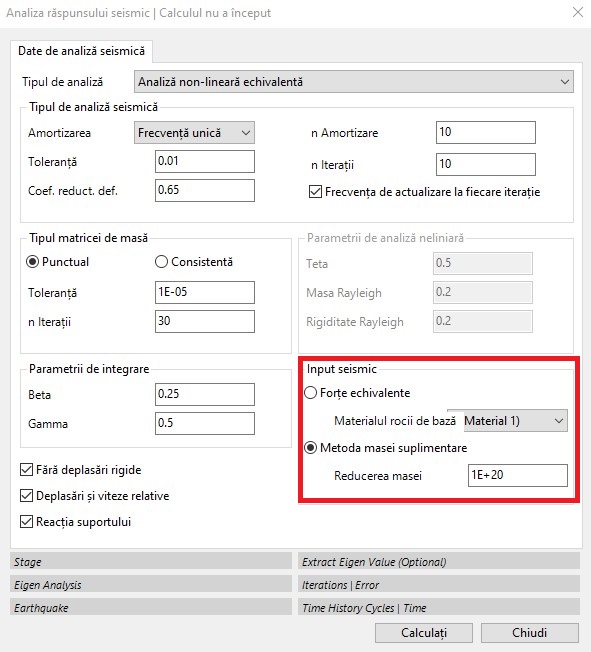
În prima abordare, contribuția seismică este definită în termeni de forțe nodale echivalente (sau forțe seismice efective), care sunt proporționale cu viteza undelor incidente și sunt aplicate în direcția orizontală de-a lungul bazei domeniului definit de model. Acest tip de aport seismic (aport seismic la suprafață) este considerat o forță de forfecare temporală:
F(t) = ρVsAv(t)
Unde ρ este densitatea rocii, Vs reprezintă viteza undei S în rocă, v(t) reprezintă viteza de propagare a cutremurului, iar A reprezintă contribuția areală asociată nodului încărcat.
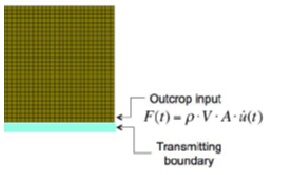
Abordare seismică Forțe echivalente
Aceste forțe sunt calculate automat de software și sunt aplicate la nodurile din domeniu aflate în contact cu roca de bază, astfel încât avantajul acestei metode constă tocmai în faptul că nu trebuie să se modeleze stratul de rocă de bază, ci trebuie doar să se aleagă materialul din care este făcută. Prin selectarea acestei metode, condițiile limită din etapa 1 sunt reprezentate prin arcuri atât pe orizontală, cât și pe verticală pentru toate nodurile la contur ale domeniului. În etapa 2, programul calculează automat efectele arcurilor pentru toate contururile domeniului.
©GeoStru