Zeng and Liang carried out a series of parametric analyzes of a two-dimensional model developed by finite element code, which reproduces the case of drilled shafts (piles immersed in a moving soil).
The two-dimensional model reproduces a slice of soil of unit thickness and assumes that the phenomenon occurs in plane strain conditions in the direction parallel to the axis of the piles.
The model was used to investigate the influence on the formation of an arch effect of some parameters such as the distance between the piles, the diameter and the shape of the piles, and the mechanical properties of the soil. The authors identify the relation between the distance and the diameter of the piles (s/d), the dimensionless parameter determining the formation of the arch effect.
The problem appears to be statically indeterminate, with degree of indeterminacy equal to (8n-4), but in spite of this it is possible to obtain a solution by reducing the number of unknowns and thus taking simplifying assumptions, in order to make determined the problem.
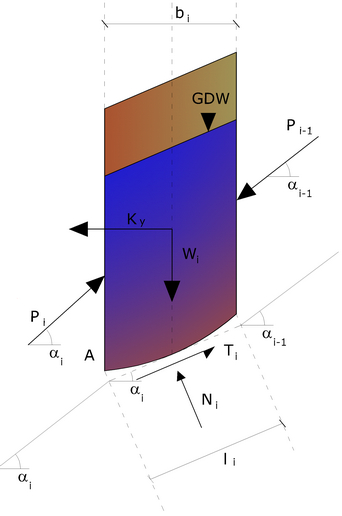
Actions on the i-th slice according to Zeng Liang
The assumptions that make the problem determined are:
•Ky are taken horizontal to reduce the total number of unknowns with (n-1) to (7n-3);
•Le normal forces at the base of the strip acting in the midpoint, reducing the unknowns with n to (6n-3);
•The position of the lateral thrusts is to one-third of the average height of inter-slice and reduces the unknowns with (n-1) to (5n-2);
•The forces (Pi-1) and Pi are assumed parallel to the inclination of the base of the strip (αi), reducing the unknowns with (n-1) to (4n-1);
•It is assumed a single yield constant for all the slices, reducing the unknowns with (n) to (3n-1);
The total number of unknowns is then reduced to (3n), to be calculated using the factor of load transfer. Furthermore, it should be noted that the stabilization force transmitted on the soil downstream of the piles is reduced by an amount R, called reduction factor, calculated as:
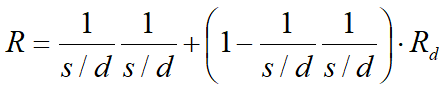
The factor R therefore depends on the ratio between the distance present between the piles and the diameter of the piles and by the factor Rd which takes into account the arch effect.
© GeoStru