El Método de la Espiral Logarítmica, introducido por Taylor en 1937, es una técnica analítica empleada en el análisis de estabilidad de taludes.
Principios Fundamentales y Ventajas
•En este método se supera la dificultad de tener que asumir arbitrariamente la distribución de las fuerzas a lo largo de la superficie de rotura. Este es un problema común en otros métodos de equilibrio límite, como el método del círculo de fricción o el método de las dovelas.
•La propiedad clave de la espiral logarítmica reside en que la resultante de las fuerzas normales y de las fuerzas de fricción pasa siempre por el origen de la espiral.
•En consecuencia, cuando se calcula el momento con respecto al origen de la espiral, el efecto combinado de las fuerzas normales y de fricción es nulo. Esto simplifica notablemente el cálculo, ya que solo quedan por considerar los momentos debidos al peso del terreno y a la cohesión.
•Esta característica lo convierte en un "punto de referencia" (yardstick) para verificar la precisión de otros métodos de análisis, dado que satisface el equilibrio de momentos sin suposiciones adicionales, aparte de la forma de espiral logarítmica de la superficie de rotura.
Ecuación de la Espiral Logarítmica
La ecuación de una espiral logarítmica en coordenadas polares se expresa como: r = ro e(θ * tan φ)
Donde:
•r es el radio desde el origen hasta la espiral logarítmica.
•r0 es el radio inicial.
•θ es el ángulo (en radianes) entre el radio inicial y el radio r. La longitud del radio aumenta si θ se mide en el sentido de las agujas del reloj; disminuye si se mide en sentido contrario a las agujas del reloj (θ negativo).
•φ es el ángulo de fricción interna del terreno. La forma de la espiral logarítmica está controlada por ϕ. Una línea normal a la espiral logarítmica siempre forma un ángulo ϕ con la línea radial.
El origen de la espiral logarítmica se localiza mediante dos ángulos arbitrarios t y z.
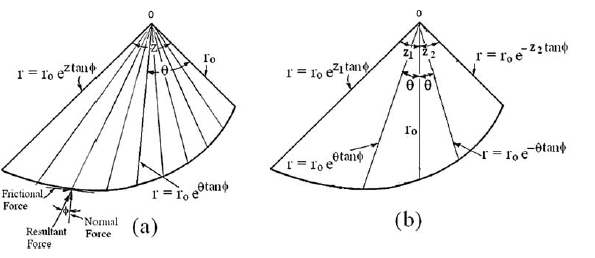
Características de la espiral logarítmica
Al utilizar el método del círculo de fricción o el método de las dovelas, la distribución de las fuerzas a lo largo del arco de rotura o en los lados de una dovela debe asumirse de manera arbitraria. Esta dificultad puede superarse si se utiliza una espiral logarítmica como superficie de rotura.
Independientemente de la magnitud de las fuerzas normales sobre la superficie de rotura, la propiedad de la espiral logarítmica es tal que la resultante de las fuerzas normales y de fricción pasa siempre por el origen de la espiral. En consecuencia, al calcular el momento con respecto al origen, el efecto combinado de las fuerzas normales y de fricción es nulo, y solo deben considerarse los momentos debidos al peso y a la cohesión. Este método de la espiral logarítmica fue propuesto por primera vez por Taylor (1937) para el análisis de estabilidad.
Cómo configurar una superficie de deslizamiento en espiral logarítmica en Slope
1.Definir la geometría de la sección y su estratigrafía.
2.Definir las coordenadas de los vértices superior e inferior y el número de filas de la superficie de deslizamiento. Es posible definir estos parámetros gráficamente cambiando a una superficie circular, dibujar la malla de centros y luego volver a una superficie genérica: el software guardará los datos.
3.Definir las coordenadas del punto de paso de las espirales logarítmicas: se debe introducir un punto adecuado al perfil de la sección.
4.Pulsar Generar, y opcionalmente configurar "Adaptar la espiral al perfil" para eliminar los tramos de espiral que queden fuera de la sección.
5.Opcionalmente, aumentar la densidad del número de puntos de las espirales, el número de filas y columnas de la malla de centros o las coordenadas de esta última.
6.Realizar el cálculo.
© GeoStru Software