El método del equilibrio límite consiste en el estudio de un cuerpo rígido, constituido por el talud y por una superficie de deslizamiento de cualquier forma (línea recta, arco circular, espiral logarítmica), véase Fig. 1. Con tal equilibrio se calculan las tensiones de corte (τ) y se comparan con la resistencia disponible (τf), calculada según el criterio de rotura de Coulomb: de esta comparación deriva la primera indicación de estabilidad, con el coeficiente de seguridad
F =τf /τ
Entre los métodos del equilibrio último hay algunos que consideran el equilibrio global del cuerpo rígido (Culman) mientras que otros, por falta de homogeneidad, dividen el cuerpo en rebanadas y consideran el equilibrio de cada una de estas (Fellenius, Bishop, Janbu etc....).
Representación de una sección de cálculo de un talud
Método de las rebanadas
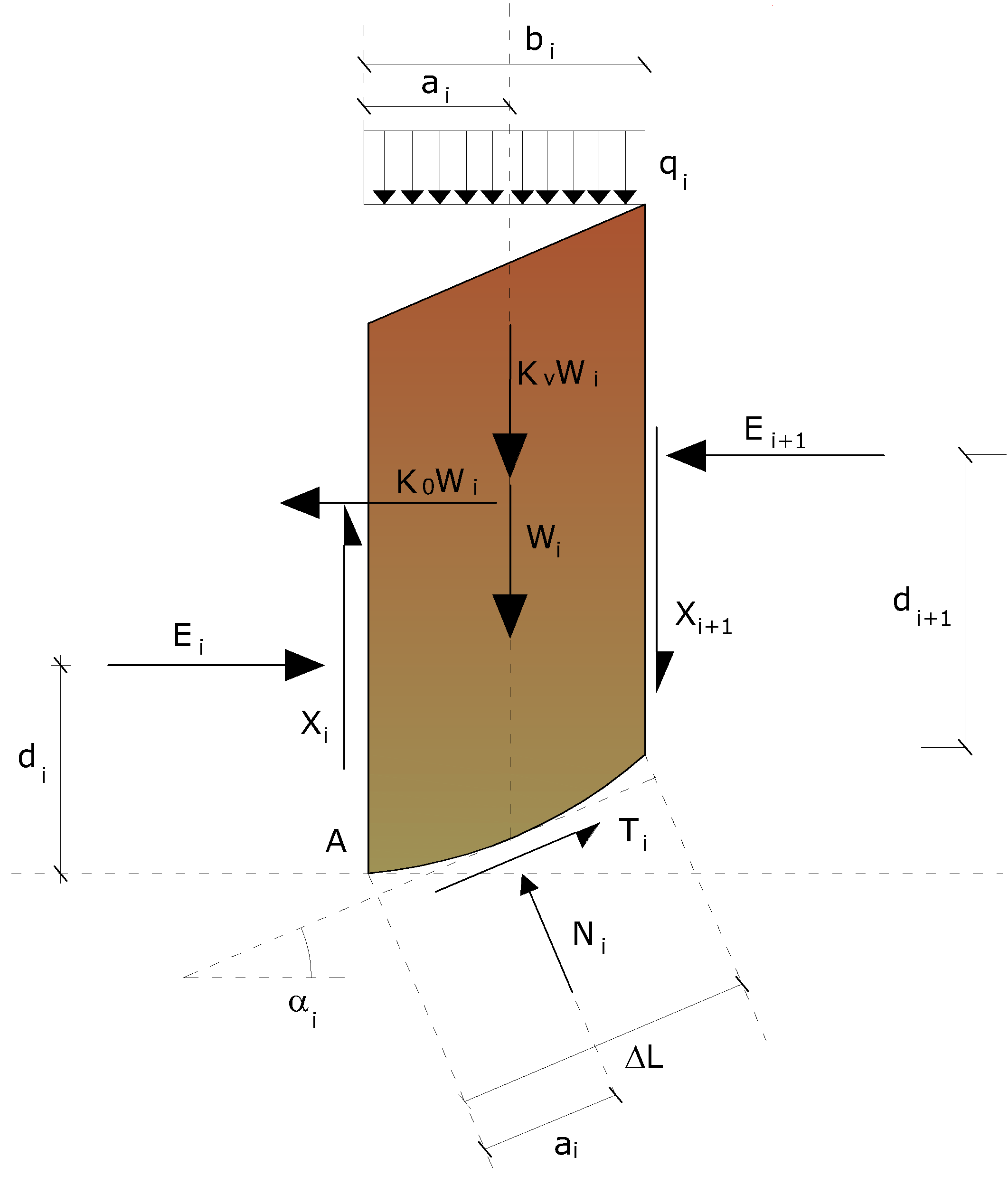
La masa susceptible al deslizamiento se subdivide en un número conveniente de rebanadas. Si el número de rebanadas es igual a n, el problema presenta las siguientes incógnitas:
•n valores de las fuerzas normales Ni en la base de cada rebanada
•n valores de las fuerzas de corte en la base de la rebanada Ti;
•(n-1) fuerzas normales Ei en la conexión de las rebanadas;
•(n-1) fuerzas tangenciales Xi en la conexión de las rebanadas;
•n valores de la coordenada "a" del punto de aplicación de las Ei;
•(n-1) valores de la coordenada del punto de aplicación de las Xi;
•una incógnita constituida por el factor de seguridad F.
En total las incógnitas son (6n-2).

Acciones en la i-ésima rebanada
Mientras las ecuaciones a disposición son:
•Ecuaciones de equilibrio de momentos n;
•Ecuaciones de equilibrio en la traslación vertical n;
•Ecuaciones de equilibrio en la traslación horizontal n;
•Ecuaciones del criterio de rotura n;
•Total número de ecuaciones 4n
El problema es estáticamente indeterminado y el grado de indeterminación es igual a
i = (6n-2)-(4n) = 2n-2.
El grado de indeterminación se reduce a (n-2) Al asumir que Ni se aplica en el punto medio de la franja, esto equivale a crear la hipótesis de que las tensiones normales totales están distribuidas uniformemente, véase figura.
Los diferentes métodos que se basan en la teoría del equilibrio límite se diferencian por el modo en que se eliminan las (n-2) indeterminaciones.
© GeoStru Software