Interconexión entre bloques
Con este método el suelo se modela como una serie de elementos discretos, que a continuación llamaremos bloques, teniendo en cuenta la compatibilidad entre los mismos.
A tal efecto cada bloque se conecta con los bloques adyacentes y con la base por medio de resortes (modelo de Winkler)
Hay una serie de resortes en dirección normal a la superficie de contacto con el fin simular la rigidez normal y otra serie en dirección tangencial para simular la resistencia al deslizamiento en la superficie de contacto.
Se asume un comportamiento elasto-plástico perfecto de los resortes normales y transversales. Los resortes normales no ceden a la compresión, ceden solo a la tracción, con una capacidad de extensión máxima en caso de suelo cohesivo y nula para suelos sin cohesión.
Los resortes transversales ceden cuando se alcanza la máxima resistencia al corte y se hace necesario distinguir dos tipos diferentes de comportamiento: suelo frágil y suelo duro. En los suelos frágiles la resistencia pico al corte de los resortes está dada por:
![]()
Mientras la resistencia residual:
![]()
Para simplificar, en el siguiente análisis se asume que después de haber alcanzado la resistencia de pico, la resistencia del suelo se reduce inmediatamente al valor de la resistencia residual.
Con suelos que no son frágiles, la resistencia no se reduce en caso de grandes deformaciones por cizalladura, por lo tanto la resistencia residual es igual a la de pico.
El planteamiento de este método sigue el de un estudio realizado precedentemente por Chang y Mistra sobre la mecánica de las partículas discretas.
Poniendo uia, uib, e ωa, ωbb en modo tal que representen el desplazamiento y la rotación de los bloques A y B, se toma el punto P de manera que sea el punto medio de la interconexión entre los dos bloques, tal como se muestra en la Fig. 5. Llamamos riap al vector que une el baricentro del bloque A con el punto P. El desplazamiento del bloque B respecto al bloque A, en el punto P se expresa entonces como sigue:
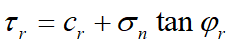
Si el bloque B se mantiene inmóvil, los valores de uxb, uyb, e ωb se asumen iguales a cero.
Tomamos nip de manera tal que sea el vector normal en la cara del bloque A en el punto P, hacia el interior definido por nip = (cosα , sinα ) donde a es el ángulo entre los ejes x y el vector nip. El vector sip, perpendicular al vector nip, estará definido por sip = (-sinα, cosα ).
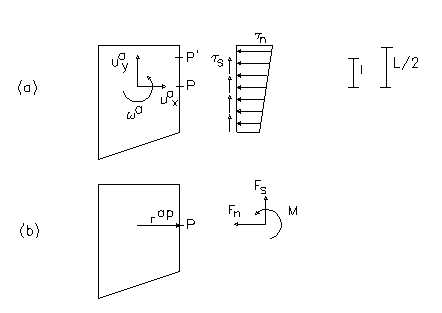
Fig. 5 (a) tensiones normales y tangenciales (b) Fuerzas y momentos equivalentes a la interconexión.
El vector deslizamiento del lado izquierdo de la ecuación 3 se puede transformar de coordenadas x-y a coordinadas locales n-s como sigue:
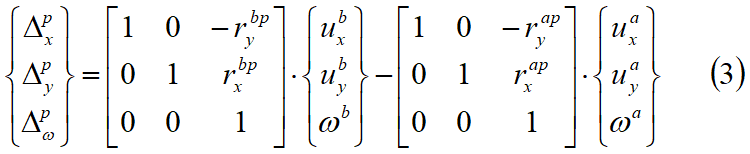
Debido al desplazamiento relativo entre dos bloques cercanos, para un punto genérico P' de la interconexión, distante l del punto central P como se muestra en la figura 5, el alargamiento del resorte en dirección normal dn y el alargamiento en dirección ds tangencial están dados por:
![]()
Por efecto del alargamiento de los resortes surgen tensiones normales tangenciales de acuerdo con el comportamiento según Winkler, como se muestra en la figura 5. Tales tensiones en la superficie de contacto se pueden integrar para obtener fuerzas y momentos resultantes equivalentes de la siguiente manera:
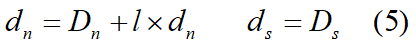
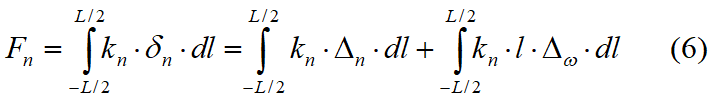
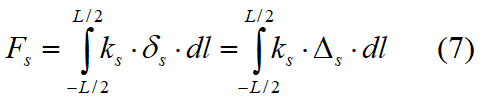
donde
kn = constante del resorte normal por unidad de longitud
ks = constante del resorte transversal por unidad de longitud
L = longitud de la interconexión
Nótese que los resortes son de tipo elasto-plástico, por lo que los valores de kn y ks están en función de la deformación y por lo tanto se deben obtener de las curvas esfuerzos deformaciones mostradas en la Fig. 2-3. Para las conexiones que no ceden se utilizan las constantes elásticas kn y ks . Con las que ceden no se pueden utilizar las constantes elásticas, por lo que se requiere un método para considerar la no linealidad del problema y para esto se usa el método de la rigidez secante. Las constantes equivalentes `kn y ` ks se pueden obtener como las correspondiente a la deformación, como se muestra en la Fig. 6
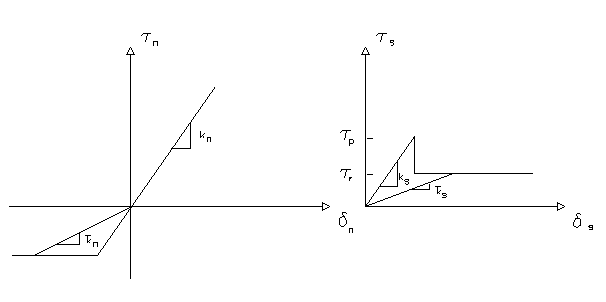
Fig. 6. Método secante para obtener Kn, Ks
Integrando tales expresiones, dado que los términos que incluyen el primer orden Kn× l son nulos se obtiene:
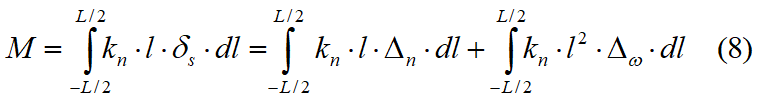
o sea, en forma de matriz:
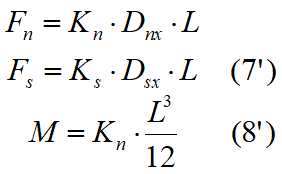
donde:
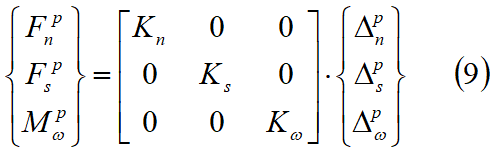
Por conveniencia, transformamos las fuerzas de conexión FnP e FsP in FxP e FyP , pasando respectivamente del sistema de coordenadas locales n-s al sistema global x-y de la siguiente manera:
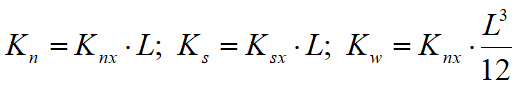
Las fuerzas resultantes agentes en cada cara de un bloque deben satisfacer las condiciones de equilibrio dadas por:
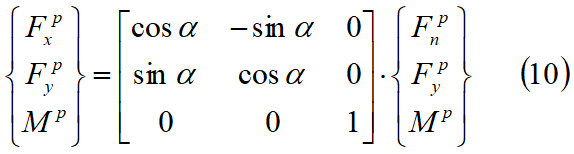
donde N es el número total de caras del bloque. Las variables fxa, fya, ma son las fuerzas y los momentos de masa gravitacional del bloque A. Combinando las ecuaciones 3, 4, 9, 10 y 11 obtenemos un nexo entre fuerzas y deslizamientos del bloque A como se indica a continuación:
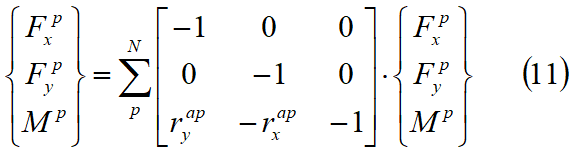
la matriz [c] está dada por el producto de las siguientes matrices:
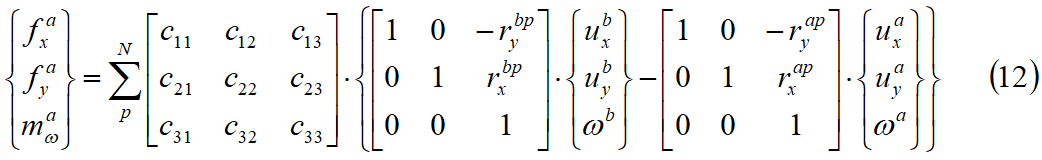
Basándonos en la ecuac. 12, con cada bloque podemos escribir las tres ecuaciones de equilibrio de las fuerzas y de los momentos, obteniendo un sistema de 3 x N ecuaciones, para N bloques, como a continuación:
{ f } =[G]× { u } (14)
{ f } : compuesta por fx, fy e m, para cada bloque
{ u } : compuesta por ux, uy ed ω , para cada bloque
[G]: la matriz de rigidez total.
Por lo tanto para cada bloque tenemos seis variables: las fuerzas de masa fx, fy e m y los deslizamientos ux, uy y la rotación ω, de las cuales se conocen tres o sea: fx y m son iguales a cero.
Resolviendo el sistema de las 3× N ecuaciones se obtienen las 3× N incógnitas.
Hallados los deslizamientos baricéntricos de cada bloque, con la ecuación 3 se pueden obtener los alargamientos de los resortes entre dos bloques adyacentes. De estos alargamientos, a través de las relaciones fuerzas-alargamientos (ecuac. 4 y 9), se pueden obtener las fuerzas normales y tangenciales. Por último se pueden encontrar las tensiones normales σn y tangenciales τs agentes en cada conexión entre dos bloques, dividiendo las fuerzas obtenidas entre el área de conexión, o sea:
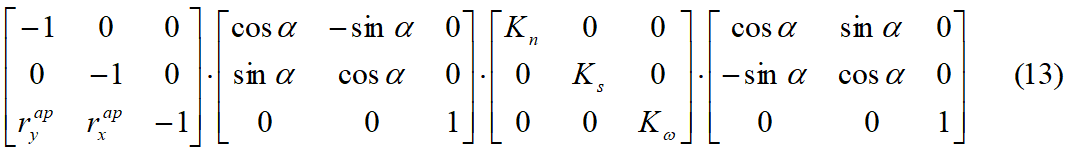
© GeoStru Software