Il metodo dell'equilibrio limite consiste nello studiare l'equilibrio di un corpo rigido, costituito dal pendio e da una superficie di scorrimento di forma qualsiasi (linea retta, arco di cerchio, spirale logaritmica, ecc.), da tale equilibrio vengono calcolate le tensioni da taglio (τ) e confrontate con la resistenza disponibile (τf), valutata secondo il criterio di rottura di Coulomb, da tale confronto ne scaturisce la prima indicazione sulla stabilità attraverso il coefficiente di sicurezza
F =τf /τ
Tra i metodi dell'equilibrio limite alcuni considerano l'equilibrio globale del corpo rigido (Culman), altri a causa della non omogeneità dividono il corpo in conci considerando l'equilibrio di ciascuno (Fellenius, Bishop, Janbu ecc.).
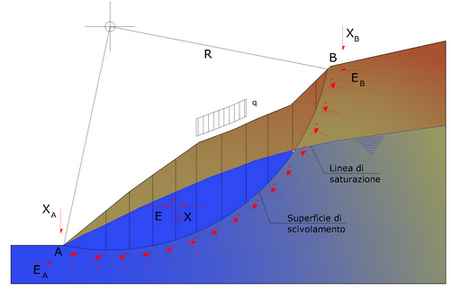
Rappresentazione di una sezione di calcolo di un pendio
Metodo dei conci
La massa interessata dallo scivolamento viene suddivisa in un numero conveniente di conci. Se il numero dei conci è pari a n, il problema presenta le seguenti incognite:
•n valori delle forze normali Ni agenti sulla base di ciascun concio;
•n valori delle forze di taglio alla base del concio Ti;
•(n-1) forze normali Ei agenti sull'interfaccia dei conci;
•(n-1) forze tangenziali Xi agenti sull'interfaccia dei conci;
•n valori della coordinata "a" che individua il punto di applicazione delle Ei;
•(n-1) valori della coordinata che individua il punto di applicazione delle Xi;
•una incognita costituita dal fattore di sicurezza F.
Complessivamente le incognite sono (6n-2).
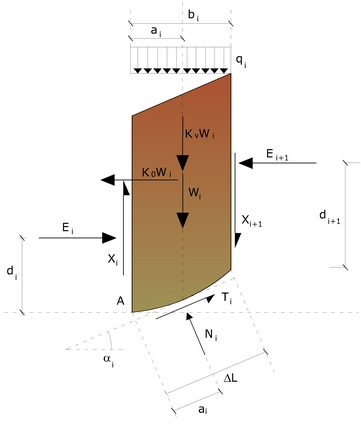
Azioni sul concio i-esimo
•mentre le equazioni a disposizione sono:
•Equazioni di equilibrio dei momenti n;
•Equazioni di equilibrio alla traslazione verticale n;
•Equazioni di equilibrio alla traslazione orizzontale n;
•Equazioni relative al criterio di rottura n;
•Totale numero di equazioni 4n
Il problema è staticamente indeterminato ed il grado di indeterminazione è pari a
i = (6n-2)-(4n) = 2n-2.
Il grado di indeterminazione si riduce ulteriormente a (n-2) in quando si fa l'assunzione che Ni sia applicato nel punto medio della striscia, ciò equivale ad ipotizzare che le tensioni normali totali siano uniformemente distribuite, vedi figura.
I diversi metodi che si basano sulla teoria dell'equilibrio limite si differenziano per il modo in cui vengono eliminate le (n-2) indeterminazioni.
© GeoStru