Metoda Spiralei Logaritmice, introdusă de Taylor în 1937, este o tehnică analitică utilizată în analiza stabilității versanților.
Principii Fundamentale și Avantaje
•Prin această metodă, se depășește dificultatea de a trebui să se presupună în mod arbitrar distribuția forțelor de-a lungul suprafeței de rupere. Aceasta este problemă comună în alte metode de echilibru limită, cum ar fi metoda cercului de frecare sau metoda fâșiilor.
•Proprietatea cheie a spiralei logaritmice constă în faptul că rezultanta forțelor normale și a forțelor de frecare trece întotdeauna prin originea spiralei.
•În consecință, atunci când se calculează momentul față de originea spiralei, efectul combinat al forțelor normale și de frecare este nul. Acest lucru simplifică considerabil calculul, deoarece rămân de luat în considerare doar momentele datorate greutății solului și coeziunii.
•Această caracteristică o face un "punct de referință" (yardstick) pentru a verifica acuratețea altor metode de analiză, dat fiind că satisface echilibrul momentelor fără ipoteze suplimentare, în afara formei de spirală logaritmică a suprafeței de rupere.
Ecuația Spiralei Logaritmice
Ecuația unei spirale logaritmice în coordonate polare este exprimată astfel: r = ro e(θ * tan φ)
Unde:
•r este raza de la origine la spirala logaritmică.
•ro este raza inițială.
•θ este unghiul (în radiani) între raza inițială și raza r. Lungimea razei crește dacă θ este măsurat în sens orar; scade dacă este măsurat în sens antiorar (θ negativ).
•φ este unghiul de frecare internă al solului. Forma spiralei logaritmice este controlată de φ. O linie normală la spirala logaritmică formează întotdeauna un unghi φ cu linia radială.
Originea spiralei logaritmice este localizată prin intermediul a două unghiuri arbitrare t și z.
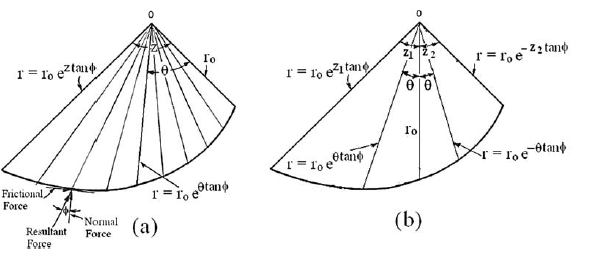
Caracteristicile spiralei logaritmice
La utilizarea metodei cercului de frecare sau a metodei fâșiilor, distribuția forțelor de-a lungul arcului de rupere sau pe laturile unei fâșii trebuie presupusă în mod arbitrar. Această dificultate poate fi depășită dacă se utilizează o spirală logaritmică drept suprafață de rupere.
Indiferent de mărimea forțelor normale pe suprafața de rupere, proprietatea spiralei logaritmice este astfel încât rezultanta forțelor normale și a celor de frecare trece întotdeauna prin originea spiralei. În consecință, la calcularea momentului față de origine, efectul combinat al forțelor normale și de frecare este nul și trebuie luate în considerare doar momentele datorate greutății și coeziunii. Această metodă a spiralei logaritmice a fost propusă pentru prima dată de Taylor (1937) pentru analiza stabilității.
Cum se configurează o suprafață de alunecare în formă de spirală logaritmică în Slope
1.Definiți geometria secțiunii și stratigrafia acesteia.
2.Definiți coordonatele vârfurilor superior, inferior și numărul de rânduri ale suprafeței de alunecare. Este posibil să definiți acești parametri grafic, trecând la o suprafață circulară, desenând grila de centre și apoi revenind la suprafața generică: software-ul va memora datele.
3.Definiți coordonatele punctului de trecere al spiralelor logaritmice: trebuie introdus un punct corespunzător profilului secțiunii.
4.Apăsați "Genera" (Generează), eventual setați "Adatta la spirale al profilo" (Ajustează spirala la profil) pentru a elimina segmentele de spirală care cad în afara secțiunii.
5.Eventual, măriți densitatea pasului numărului de puncte ale spiralelor, numărul de rânduri, coloane ale grilei de centre sau coordonatele acesteia din urmă.
6.Efectuați calculul.
© GeoStru