Interfațare între fâsii
Cu această metodă terenul este modelat ca o serie de elemente discrete (fâșii) și ține cont de compatibilitatea reciprocă dintre fâșii. În acest scop fiecare fâșie și fâșiile adiacente și baza sunt blocate de resorturi Winkler.
Există o serie de resorturi în direcție normală la interfață pentru a simula rigiditatea normală și o serie de resorturi în direcție tangențială pentru a simula rezistența la alunecare a interfeței.
Componenta resorturilor normale și a celor transversale se ia de tip elasto-plastic perfect.
Resorturile normale nu cedează la compresiune ci doar la tracțiune cu o capacitate extensională maximă pentru teren coeziv și fără capacitate extensională pentru terenuri necoezive.
Resorturile transversale cedează când se ajunge la rezistenta maximă de forfecare și se disting două tipuri de comportamente diferite: teren fragil și teren nefragil. Pentru teren fragil rezistența maximă a resorturilor este dată de:
![]()
În timp ce rezistența reziduală:
![]()
Pentru simplificare în analiza de mai jos s-a presupus că după ce se ajunge la rezistența maximă, rezistența terenului se trece la valoarea rezistenței reziduale.
Pentru teren nefragil rezistența nu se reduce pentru deformări mari la forfecare, deci rezistența reziduală este egală cu cea maximă.
Formularea metodei expuse are la bază o cercetare anterioară a lui Chang și Mistra asupra mecanicii discretelor deosebite.
Luându-se uia, uib, e ωa, ωb astfel încât acestea să reprezinte deplasarea și respectiv rotația fâșiilor A și B, se ia punctul P care este punctul mediu a interfeței dintre cele două fâșii, după cum se vede în Fig. 7.1.1. Fiind riap vectorul ce unește baricentrul fâșiei A cu punctul P, deplasarea fâșiei B față de fâșia A, în punctul P este exprimată ca:
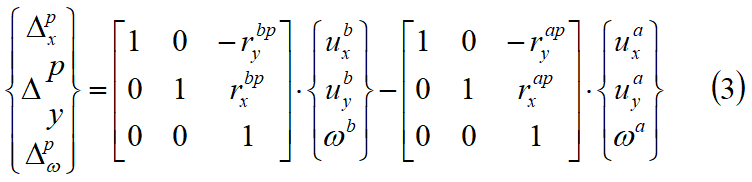
Dacă fâșia B este imobilă, valorile lui uxb, uyb, e ωb se iau egale cu zero.
Luâm nip astfel încât acesta să fie vectorul normal pe fața fâșiei A în punctul P, spre interior definit de nip = (cosα, sinα) unde a este unghiul dintre axa X și vectorul nip. Vectorul sip, perpendicular pe vectorul nip, va fi definit de sip = (-sinα, cosα).
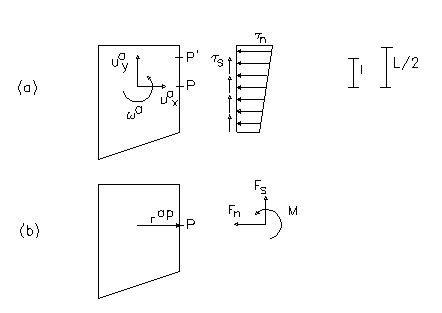
Figura 7.1.1 (a) Tensiuni normale și tangențiale ; (b) Forțe și momente echivalente la interfață
Vectorul deplasare al primului membru al Ec. 3 poate fi transformate de coordonatele X-Y în coordonate locale n-s după cum urmează:
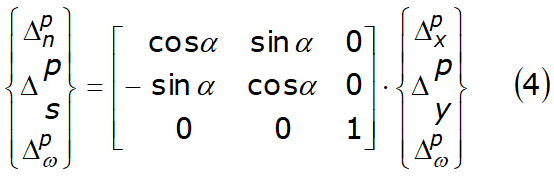
Datorită deplasării relative dintre fâșiile vecine, pentru un punct generic P' al interfeței, la distanță l de la punctul central P după cum este evidențiat în Fig. 7.1.1, alungirea resortului în direcția normală dn și cea în direcția tangențială ds sunt date de:
![]()
Datorită efectului alungirii resorturilor apar tensiuni normale și tangențiale în acord cu comportamentul Winkler, după cum se vede în Fig. 7.1.1. Aceste tensiuni pe interfață pot fi integrate pentru a obține forțe și momente rezultante echivalente după cum urmează:
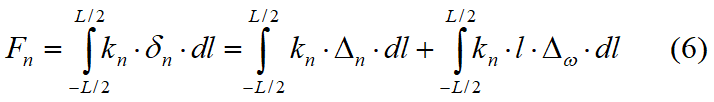
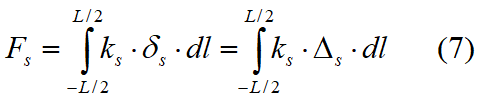
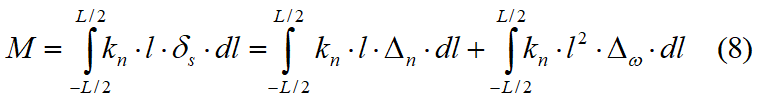
unde:
kn = constanta resortului normal pe unitatea de lungime
ks = constanta resortului transversal pe unitatea de lungime
L = lungimea interfeței
Resorturile sunt de tip elasto-plastic deci valorile lui kn și ks sunt în funcție de deformare, deci trebuie să se obțină din curbele eforturi-deformații reprezentate în Fig. X.Y.2. Pentru interfețe care nu cedează se folosesc constantele elastice kn și ks . Pentru cele care cedează constantele elastice nu pot fi folosite, deci este solicitată o metodă pentru a considera neliniaritatea problemei. În acest scop se folosește metoda rigidității secante. Constantele echivalente ` kn și ` ks pot fi obținute precum cele corespondente deformării interfeței, ca și în Fig. 7.1.2.
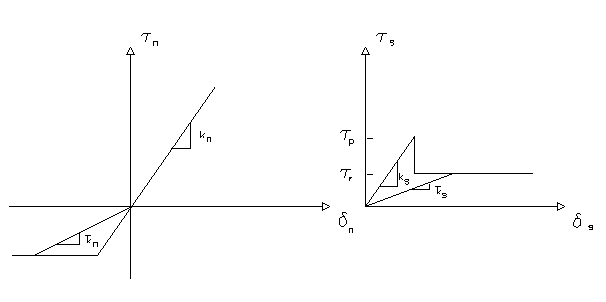
Figura 7.1.2 - Reprezentarea metodei rigidității secante, definirea constantelor echivalente 'Kn, 'Ks
Integrând aceste expresii, având în vedere faptul că termeni ce includ primul ordin Kn× L sunt nuli se obține:
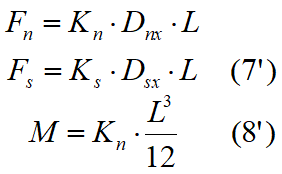
sau, în forma matricială:
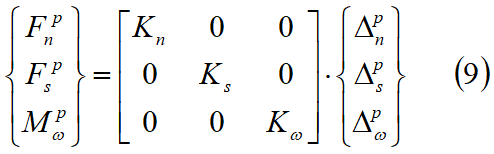
unde:
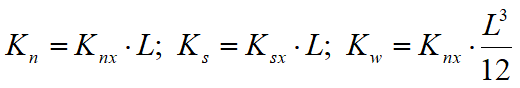
Pentru comoditate transformăm forțele de interfață FnP și FsP în FxP și FyP, trecând de la sistemul de coordonate locale n-s la sistemul global X-Y după cum urmează:
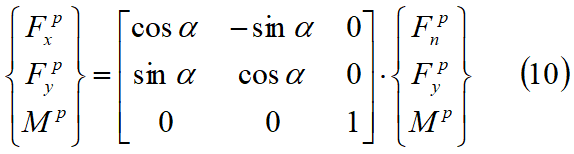
Forțele rezultante ce acționează pe fiecare față a fâșiei trebuie să satisfacă următoarele condiții de echilibru:
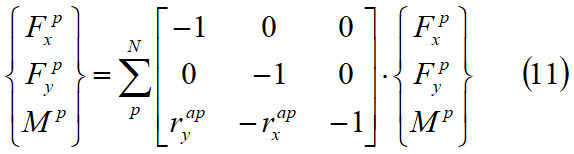
unde N este numărul total de fețe ale fâșiei. Variabilele fxa, fya mai sunt forțele și momentele de masă gravitațională a fâșiei A. Combinând ecuațiile 3, 4, 9, 10 și 11 obținem o legătură între forțe și deplasările fâșiei A după cum urmează:
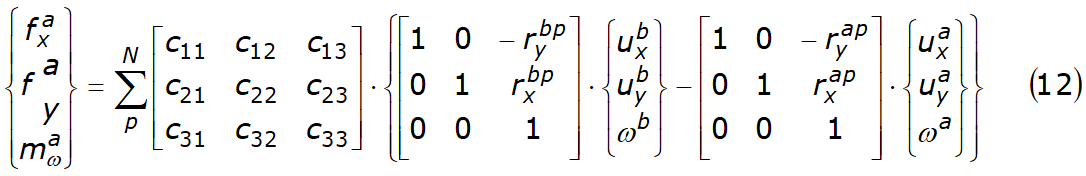
matricea [c] este dată de produsul următoarelor matrici:
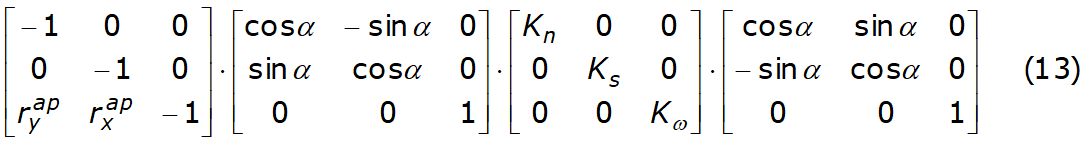
Făcând referire la Ec. 12, pentru fiecare fâșie putem scrie cele trei ecuații de echilibru a forțelor și momentelor, obținând un sistem de 3 × N ecuații, pentru N fâșii, fiind exprimat ca:
![]()
{ f }: este compusă din fx, fy și m, pentru fiecare fâșie
{ u }: este compusă din ux, uy ed ω, pentru fiecare fâșie
[G]: este matricea de rigiditate totală
Deci pentru fiecare fâșie avem șase variabile, forțele de masă fx, fy și m, deplasările ux, uy și rotația ω, dintre care trei sunt cunoscute, adică fx și m sunt egale cu zero.
Rezolvând sistemul 3 × N ecuații se găsesc cele 3 x N necunoscute.
O dată aflate deplasările baricentrului fiecărei fâșii, prin intermediul ecuației 3 se pot afla alungirile resorturilor între două fâșii adiacente. De la aceste alungiți, prin intermediul relațiilor forte-alungiri (Ec. 4 și 9), se pot afla forțele normale și tangențiale. Se pot afla de asemenea tensiunile normale σn și tangențiale τs ce acționează pe fiecare interfața a celor două fâșii, împărțind forțele aflate cu aria interfeței, și anume:
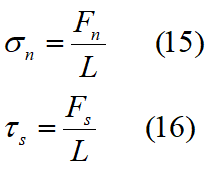
© GeoStru