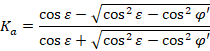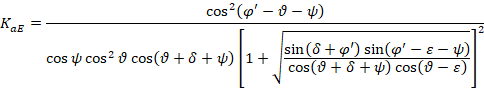<< Click to Display Table of Contents >> Navigation:  Theory > Tensile Force Acting on the Reinforcement

The tensile force acting on an individual nail, , can be assessed using the following expression, valid in the presence of a water table, under pseudo-static conditions, and assuming homogeneous soil:

 

 

Where the various terms have the following expressions:

•: Reductive coefficient

•: Effective active stress at the average depth of the influence zone of the i-th nail

•: Vertical spacing between nails; also defines the thickness of the influence zone of the i-th nail

•: Horizontal spacing between nails

•: Inclination, with respect to the horizontal direction, of the i-th nail

•: Increase in effective active stress at the average depth of the influence zone of the i-th nail due to seismic effects

•: Neutral pressure at the average depth of the influence zone of the i-th nail

 

The effective active stress is calculated based on the coefficient of active earth pressure, , the effective vertical stress acting at the depth of the considered point, , the applied surcharge load on the embankment, and the effective cohesion .

 

 

Subsequently, the coefficient of active earth pressure is calculated using the following theories:

Rankine's theory:

 

 

Coulomb's theory:

 

 

Where δ represents the angle of friction between the wall and the soil, while ϑ, defined in Figure 2, must be used in Eq. 7 with a negative sign. All other parameters have been introduced previously. Regarding the seismic stress increment, it is calculated as follows:

 

 

Where represents the effective stress at the average depth of the influence zone of the i-th nail due to seismic effects:

 

 

Where is the coefficient of active earth pressure under seismic conditions, calculated later using the Mononobe-Okabe theory:

 

 

In which

 

 

 

It is worth noting that in Eq. 4, the sum of the first and second terms could be replaced using Eq. 8. However, it has been preferred to keep the static contribution separate from the seismic increment. This allows for the application of different coefficients to the two terms if an empirical approach is desired.

 

In the case of static analysis, the second term of Eq. 4 becomes zero. In the case of dry soil, the third term becomes zero, and in the first term, the effective stress coincides with the total stress.

 

In the most general case, where the soil is stratified, depending on the position of the influence thickness of each nail with respect to the soil layers, the four different cases indicated in Figure 5 are possible.

 

Fig. 5 – Possible distributions of the total horizontal stress, , with depth depending on the position of the influence thickness of each nail with respect to the soil layers.

 

With reference to each of these cases, Figure 5 shows the variation with depth of the total horizontal stress, , which is characterized by a jump and a change in slope at the interfaces between the layers. In such situations, it is convenient to calculate the tensile force acting on the individual reinforcement as the resultant of the distribution of horizontal stresses:

 

 

Where and are the depths defining the beginning and end of the influence zone of the i-th nail. In pseudo-static conditions, in Eq. 12, it is necessary to add the term due to the seismic stress increment, using the same logic as seen in the case of homogeneous soil.