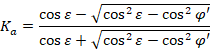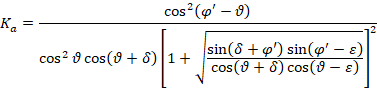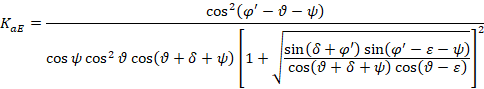La fuerza de tracción actuante en el clavo individual, F_i, puede evaluarse mediante la siguiente expresión, válida en presencia de acuífero, en condiciones pseudoestáticas y con suelo homogéneo:
|
|
(4) |
Los parámetros indicados en estas ecuaciones tienen el significado que se presenta a continuación:
kn: coeficiente reductor
σa,i': tensión efectiva activa en la profundidad media de la zona de influencia del i-esimo clavo
Sv,i: distancia entre los ejes de los clavos en la dirección vertical; define también el espesor de la zona de influencia del i-esimo clavo
Sh: distancia entre los ejes de los clavos en la dirección horizontal
αi: inclinación, en relación a la dirección horizontal, del i-esimo clavo
∆σaE,i':aumento de la tensión efectiva activa a la profundidad media de la zona de influencia del i-ésimo clavo debido al sismo
ui: presión neutra a la profundidad media de la zona de influencia del i-esimo clavo
La tensión efectiva activa se calcula en función del coeficiente de empuje activo, Ka, de la tensión efectiva vertical actuante a la profundidad del punto considerado, σv,i', de la carga eventual aplicada al terraplén q y de la cohesión efectiva c'.:
|
|
(5) |
A continuación, el coeficiente de empuje activo se calcula mediante las siguientes teorías:
teoría de Rankine:
|
|
(6) |
teoría de Coulomb:
|
|
(7) |
Donde δ representa el ángulo de fricción suelo-muro, y θ, definido en Imag. 2, se debe utilizar en la Ec. 7 con signo negativo. Todos los demás parámetros fueron introducidos previamente. Con respecto al incremento de la tensión por efecto del sismo, se calcula de la siguiente forma:
|
|
(8) |
Donde σaE,i' representa la tension eficaz a la profundidad media del área de influencia del i-esimo clavo por efecto del sisma:
|
|
(9) |
Donde KaE es el coeficiente de empuje activo en condiciones sísmicas, calculado como sigue mediante la teoría de Mononobe-Okabe:
|
|
(10) |
Donde
|
|
(11) |
Cabe señalar que en la Ec. 4, la suma del primero y del segundo término se podría reemplazar con la Ec. 8. Sin embargo,se ha preferido mantener separada la contribución estática del incremento debido al sismo, ya que en el caso de aplicar un enfoque normativo, es posible multiplicar los dos términos por coeficientes diferentes.
En caso de un análisis realizado en condiciones estáticas, el segundo término de la Ec. 4 se anula, mientras, en el caso de suelo seco, se anula el tercer término y en el primero la tensión efectiva coincide con la total.
En el caso más general, donde el suelo está estratificado, según la posición del espesor de influencia de cada clavo con respecto a las capas de suelo, son posibles los diferentes cuatro casos indicados en la Imag. 5.
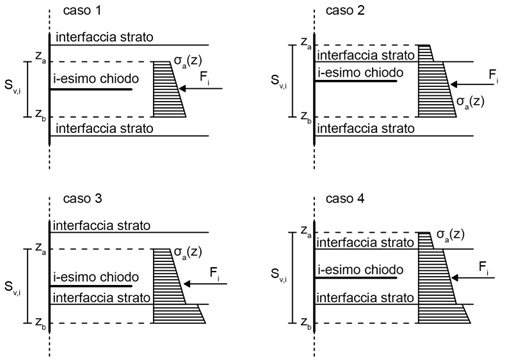
Imag. 5 – Posibles distribuciones de la tensión horizontal total, σa (z), con la profundidad según la posición del espesor de influencia de cada clavo con respecto a los estratos del suelo.
Con referencia a cada uno de estos casos, la Imag. 5 muestra la variación con la profundidad de la tensión horizontal total, σa (z), este es caracterizada por un cambio de inclinacion en las interfaces entre los estratos. Para situaciones como esta, es conveniente calcular la fuerza de tracción actuante en cada refuerzo como resultado de la distribución de las tensiones horizontales:
|
|
(12) |
Donde za y zb son las profundidades que definen el inicio y el final de la zona de influencia del i-esimo clavo.
En condiciones seudostáticas, en el Ec. 12 es necesario añadir el término causado por el aumento de tension debido al sismo, utilizando la misma lógica vista en el caso de suelo homogéneo.