La verificación por deslizamiento, en el caso de muros reforzados con la técnica del Soil Nailing, puede considerarse como un caso particular de la verificación de la estabilidad global, que puede ocurrir cuando debajo del bloque reforzado hay un estrato débil.
De acuerdo con las pautas estadounidenses FHWA-NHI-14-007, la verificación por deslizamiento se puede hacer con el mecanismo indicado en la Imag. 6.
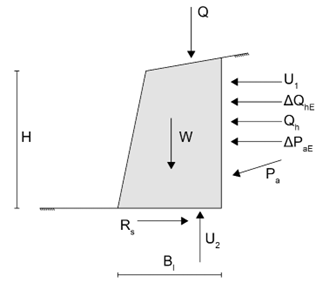
Fig. 6 – Mecanismo de rotura utilizado para realizar la verificación del deslizamiento, de acuerdo con las pautas estadounidenses FHWA-NHI-14-007.
Las acciones indicadas en el esquema de la Imagen 6 son las siguientes:
Pa: Empuje del suelo debido a su propio peso, en términos de tensiones efectivas, en condiciones estáticas
ΔPaE: Aumento del empuje del suelo en términos de tensiones efectivas debido al efecto del sismo
W: Peso de la cuña potencialmente inestable
Q: Resultante de las cargas aplicadas al nivel de campo
Qh: Resultante de las tensiones horizontales que actuan en la pared vertical, debido a las cargas aplicadas al nivel de campo, en condiciones estáticas
ΔQhE: incremento de Qh por efecto del sisma
U1: Resultante de las presiones neutras actuantes en la pared vertical
U2: Empuje hidrostático del agua
Rs: Resistencia al deslizamiento
Es necesario notar que la posición en la que estas fuerzas están representadas en la Imagen 6 es completamente indicativa, ya que la verificación se realiza utilizando las ecuaciones de equilibrio en la dirección horizontal y vertical, mientras que el equilibrio en la rotación no se impone; por lo tanto, los brazos no entran en juego.
El peso W se calcula multiplicando el peso de la unidad de volumen del bloque por el área correspondiente, mientras Q se calcula como la suma de todas las resultantes de las cargas en la dirección vertical aplicadas el nivel de campo dentro del ancho Bl. Qh se calcula como la resultante de las tensiones horizontales debidas a las cargas aplicadas sobre el nivel de campo, haciendo referencia a la teoría del semiespacio elástico. Este valor se refiere a la condición estática y, por lo tanto, es función del coeficiente de empuje activo Ka. Para el cálculo de ΔQhE se utiliza la siguiente ecuación:
|
|
(17) |
Donde QhE es el análogo de Qh, que se refiere pero a la condición pseudoestática, y se calcula entonces en función del coeficiente de empuje activo KaE. Las demás fuerzas se calculan utilizando las siguientes ecuaciones:
|
|
(18) |
Esta ecuación es válida en el caso de suelo homogéneo y seco. En presencia de un acuífero, la ecuación se modifica teniendo en cuenta adecuadamente el peso de la unidad de volumen aligerado para las porciones de suelo por debajo del nivel freático. El valor de H1 representa, sin embargo, la altura de la pared vertical interna de la cuña potencialmente inestable. Ademá:
|
|
(19) |
Donde PaE es análogo a Pa con la diferencia de que se utiliza KaE en lugar de Ka. De manera similar a las verificaciones mostradas anteriormente, Pa e ΔPaE se consideran por separado (en lugar de considerar directo PaE), de manera que se puedan utilizar diferentes coeficientes amplificadores en caso de que se desee seguir un enfoque normativo.
La resultante de las presiones neutras U1 se calcula mediante la siguiente ecuación:
|
|
(20) |
Donde d1 es la parte de H1 bajo nivel freático. Esta ecuación es válida bajo la hipótesis de que, en presencia de un nivel de campo inclinado, el nivel freático sea paralelo al plano de tierra y que haya un movimiento de filtración paralelo a él. La presión de agua U2 adquiere la siguiente expresión:
|
|
(21) |
La resistencia al deslizamiento es igual a:
|
|
(22) |
Donde cf' e φf' son respectivamente cohesión y ángulo de resistencia al corte del suelo de cimentación.
La verificación del deslizamiento consiste en asegurarse de que el respectivo coeficiente de seguridad sea mayor que la unidad. Este coeficiente se define de la siguiente manera:
|
|
(23) |
Donde
|
|
(24) |
Finalmente, es necesario tener en cuenta que la verificación se realiza en referencia a una cuña potencialmente inestable de ancho igual a Bl. Este ancho puede ser asumido o calculado. En este último caso, a continuación se consideran las siguientes opciones para el cálculo de Bl:
|
|
(25) |
|
|
(26) |
En esta ecuación, z1 representa la profundidad del primer clavo en relación con el espesor de la pared, L1 y α1 son respectivamente la longitud y la inclinación del clavo mismo.