El método de elementos finitos (MEF) es el método que cuenta con más bases teóricas sólidas y racionales. De hecho, el método presupone que el problema se trate teniendo en cuenta ya sea el aspecto estático (y por lo tanto el equilibrio del problema) que el aspecto cinemático (y por lo tanto la congruencia de los desplazamientos y deformaciones).
Con el MEF la pantalla se modela como un conjunto de vigas (elementos beam), vinculadas en continuidad al terreno por medio de resortes elásticos cuyas rigidez se estima en función de las propiedades elásticas del terreno. En la siguiente figura se muestra el esquema del modelo utilizado para el análisis con elementos finitos:
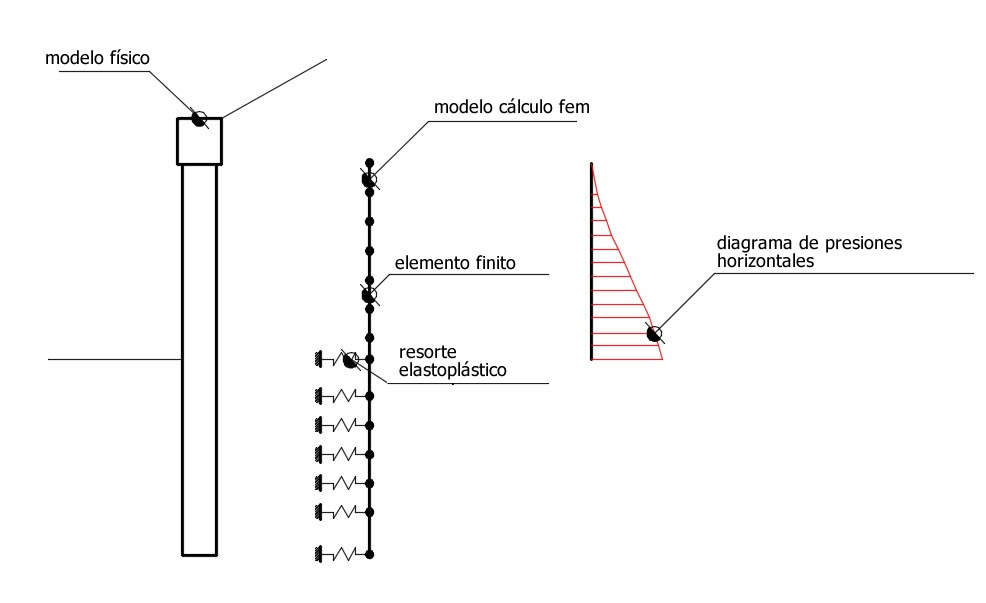
Esquema del complejo pantalla-terreno con elementos finitos
El método de elementos finitos requiere conocer las propiedades del terreno y de la estructura (a diferencia del método LEM, que establece una condición de equilibrio de cuerpo rígido). En particular, es necesario conocer el módulo de reacción del terreno. Las principales partes que componen la aplicación del método son las siguientes:
•Caracterización de los materiales y de la estructura mediante:
▪el cálculo de coeficientes de empuje activo y pasivo, además del módulo de balasto del terreno
▪el cálculo de la rigidez flexional, cortante y normal de la pantalla
•Discretización de la pantalla en elementos finitos y modelado de los resortes:
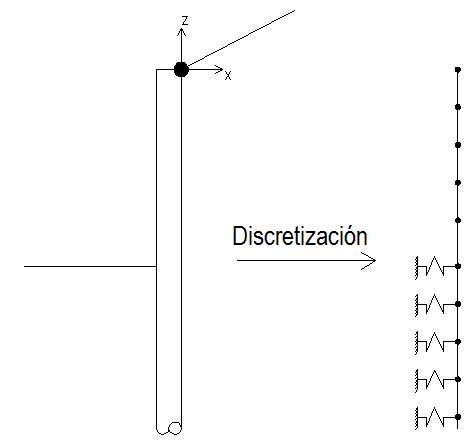
Procedimiento de discretización
•Ensamblaje de las contribuciones de cada elemento finito: En esta fase se indica el problema en su globalidad, ensamblando las contribuciones de rigidez de cada elemento finito.
•Solución del problema: El problema de elementos finitos se plantea en términos de sistema no lineal en las variables de deslizamiento. En esta etapa se establece un procedimiento iterativo que permite solucionar un problema no lineal de tipo:
![]()
En la ecuación anterior K(u) es la matriz de rigidez del problema (no lineal), u es el campo de deslizamientos que es la solución del problema y p es el vector de las cargas externas(vector asociado a la distribución de presiones del terreno).
•Ensamblaje e interpretación de la solución:
Una vez determinados los valores de los componentes del vector u se pueden derivar todas las informaciones (relativas al análisis estructural). En particular, se determinan:
▪Momento
▪Corte
▪Esfuerzo normal
© Geostru