Nel software Paratie è possibile prendere in considerazione la presenza di eventuali carichi distribuiti sul terrapieno in termini di Linee, Strisce o Carichi Uniformi. L'ambiente per la gestione di queste tipologie di carico è il seguente:
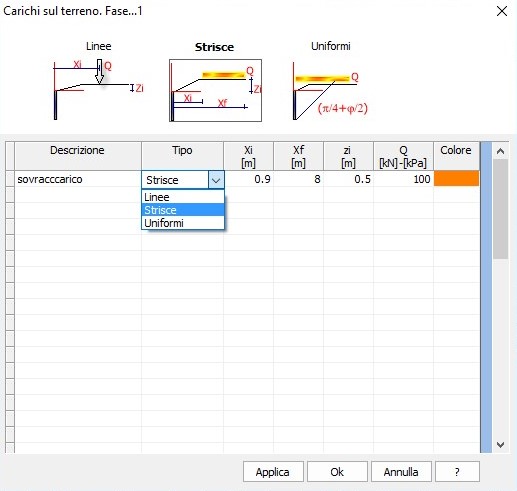
Ambiente per la gestione dei carichi distribuiti.
I dati da inserire per la corretta definizione di un carico sono i seguenti:
•Descrizione: Identifica il carico; dato necessario per l'individuazione dell'azione nelle combinazioni di carico;
•Tipo: Si può scegliere tra linee di carico, strisce di carico o carico uniformemente distribuito;
•xi: E' l' ascissa a partire dalla quale il carico inizia ad agire. Nel caso di linee di carico è l'ascissa che definisce l' applicazione della linea di carico; è espressa in m.
•xf: Tale dato è rischiesto se si definiscono strisce di carico o carichi uniformi. E' l'ascissa finale del carico (definisce quindi l'estensione del carico); è espressa in m.
•zi: Profondità espressa in m, attualmente ha solo valenza grafica, pertanto l'incremento di tensione indotto dal sovraccarico viene comunque valutato a partire dalla testa della paratia.
•Q: Intensità del carico, espressa in kN (se si tratta di linea di carico) o in kN/m² se si tratta di striscia e di carico uniforme;
•Colore: Assegnazione del colore con il quale visualizzare la striscia di carico.
N.B. I carichi si intendono distribuiti a metro lineare in direzione longitudinale.
Per l' interpretazione delle diverse tipologie di carico può essere utile osservare le seguenti figure:
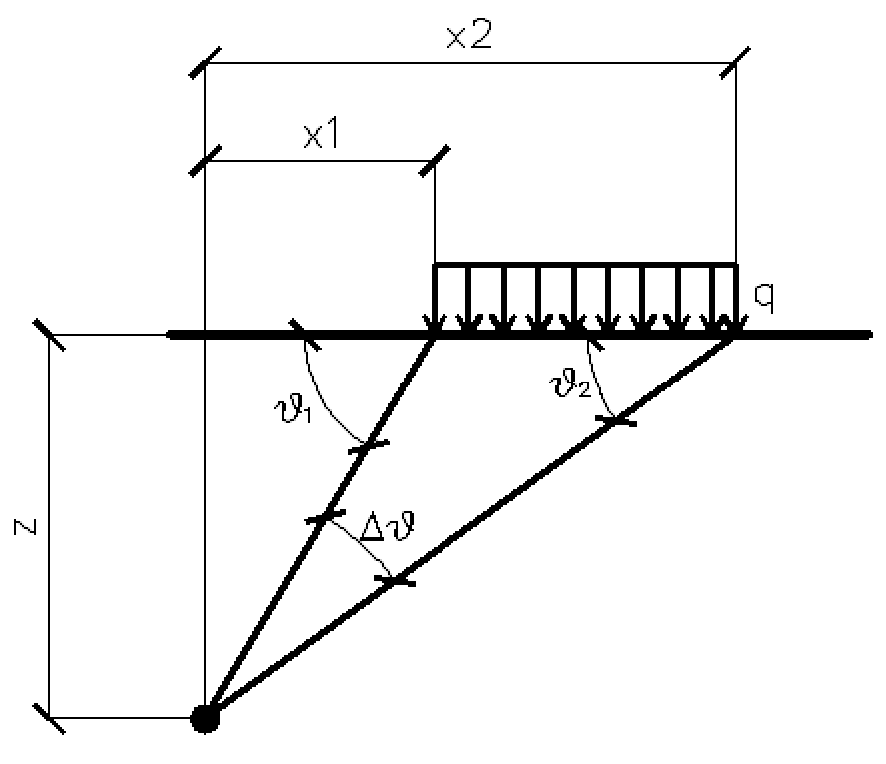
Strisce di carico ortogonali
Per le strisce di carico si valuta la distribuzione delle tensioni in funzione della profondità z.
Un carico ripartito in modo parziale con ascissa iniziale x1 ed ascissa finale x2 genera un diagramma di pressioni sulla parete i cui valori sono stati determinati secondo la formulazione di TERZAGHI, che esprime la pressione alla generica profondità z come segue:
![]()
Δϑ = ϑ1-ϑ2;
A = sen(2ϑ1)-sen(2ϑ2)
B = cos(2ϑ1)-cos(2ϑ2)
ϑ1 = arctg(z/x1)
ϑ2 = arctg(z/x2)
Per integrazione si otterrà la risultante ed il relativo braccio.
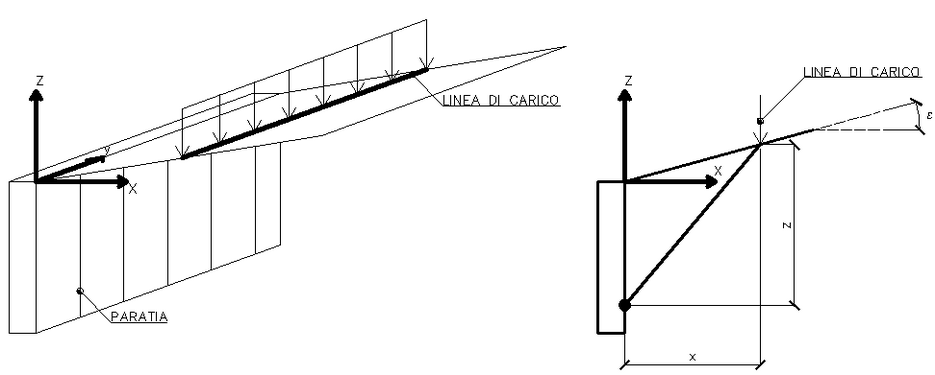
Schematizzazione delle linee di carico
Per le linee di carico, come per le strisce di carico, si valuta la distribuzione delle tensioni in funzioni della profondità z. Le linee di carico generano un incremento di pressioni sulla parete che secondo BOUSSINESQ, alla profondità z, possono essere espresse come segue:
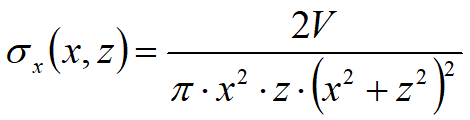
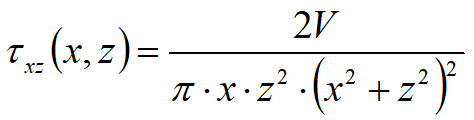
Dove i simboli hanno il seguente significato:
V = Intensità del carico espressa in [F/L];
X = Distanza, in proiezione orizzontale, del punto di applicazione del carico dalla parete;
Se il piano di azione è inclinato di e viene ruotato il sistema di riferimento (x,z) in (X,Z), attraverso la seguente trasformazione:
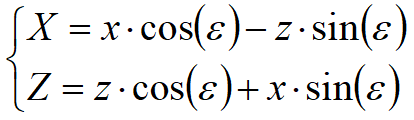
Un carico Q, uniformemente distribuito sul piano campagna induce delle pressioni costanti pari:
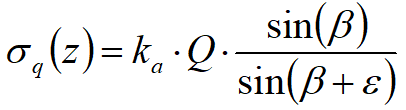
Integrando la tensione riportata alla formula precedente si ottiene la spinta totale dovuta al sovraccarico:
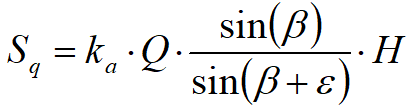
Con punto di applicazione ad H/2 (essendo la distribuzione delle tensioni costante). Nelle precedenti formule i simboli hanno il seguente significato:
β = Inclinazione della parete interna rispetto al piano orizzontale passante per il piede;
ε = Inclinazione del piano campagna rispetto al piano orizzontale positiva se antioraria;
Ka = Coefficiente di pressione attiva calcolato al paragrafo precedente.
N.B. Il carico uniforme viene distribuito in automatico dalla testa della paratia su tutta l'ampiezza del cuneo di rottura.
© GeoStru