Il metodo degli elementi finiti è il metodo che più di tutti si fonda su basi teoriche solide e razionali. Di fatto tutto il metodo presuppone che il problema sia affrontato tenendo in conto sia l’aspetto statico (e quindi l’equilibrio del problema), sia l’aspetto cinematico (e quindi la congruenza degli spostamenti o meglio delle deformazioni). Nel metodo FEM la paratia è modellata come un insieme di travi (elementi beam), con vincolo di continuità al terreno mediante molle elastiche, la cui rigidezza è valutata in funzione delle proprietà elastiche del terreno. Nella figura che segue è mostrato schematicamente il modello utilizzato per l’analisi ad elementi finiti:
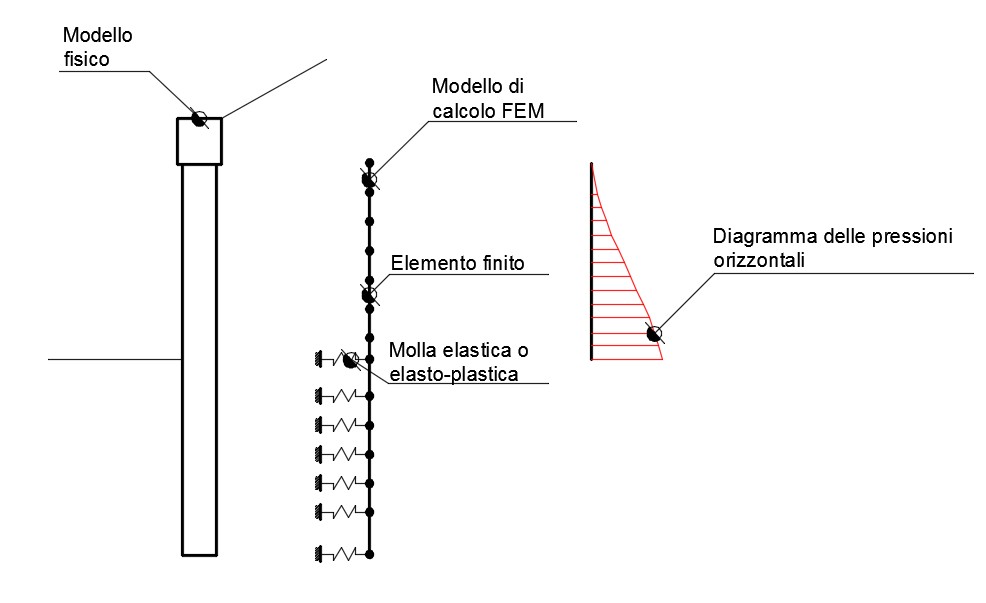
Schematizzazione del complesso paratie-terreno mediante elementi finiti
Il metodo degli elementi finiti richiede comunque la conoscenza delle proprietà del terreno e della struttura (a differenza del metodo LEM in cui si impone una condizione di equilibrio di corpo rigido). In particolare è necessario conoscere il modulo di reazione del terreno. Le principali parti in cui si articola l'applicazione del metodo sono le seguenti:
•Caratterizzazione dei materiali e della struttura mediante
▪la valutazione di coefficienti di spinta attiva e passiva, oltre che del modulo di reazione per il terreno;
▪la valutazione della rigidezza flessionale, tagliante e normale della paratia;
•Discretizzazione della paratia in elementi finiti e modellazione delle molle
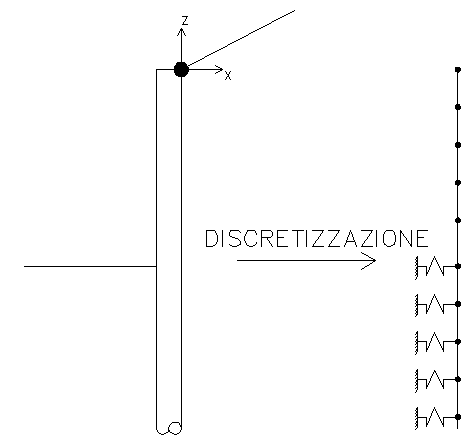
Procedimento di discretizzazione
•Assemblaggio dei contributi dei singoli elementi finiti
In questa fase si riporta il problema nel globale, assemblando i contributi di rigidezza dei singoli elementi finiti.
•Soluzione del problema
Il problema ad elementi finiti è posto in termini di sistema non lineare nelle variabili spostamento. In questa fase si imposta quindi una procedura iterativa che permette la soluzione di un problema non lineare del tipo:
![]()
Nella precedente equazione K(u) è la matrice di rigidezza del problema (di tipo non lineare), u è il campo di spostamenti che è soluzione del problema, e p è il vettore dei carichi esterni (vettore associato alla distribuzione di pressioni del terreno).
•Assemblaggio ed interpretazione della soluzione
Una volta determinati i valori delle componenti del vettore u si possono derivare tutte le informazioni (relative all' analisi strutturale). In particolare si determinano:
▪Momento;
▪Taglio;
▪Sforzo normale.
© GeoStru