Il metodo dell’equilibrio limite consiste nel ricercare soluzioni, al problema di verifica o di progetto, che siano compatibili con il solo aspetto statico del problema. In sostanza si ragiona in termini di equilibrio di un corpo rigido, senza preoccuparsi della congruenza cinematica degli spostamenti. I principali schemi di calcolo cui si farà riferimento sono i seguenti:
•Paratia a sbalzo;
•Paratia tirantata ad estremo libero;
•Paratia tirantata ad estremo fisso;
Paratia a sbalzo:
Calcolo della profondità d’ infissione limite
Per paratia non tirantata, la stabilità è assicurata dalla resistenza passiva del terreno che si trova a valle della stessa; dall' equilibrio dei momenti rispetto al centro di rotazione si ottiene:
![]()
Dove i simboli hanno il seguente significato:
Sm= componente orizzontale della spinta attiva;
Bm= braccio di Sm rispetto ad O centro di rotazione;
Rv= componente orizzontale della resistenza passiva;
Bv= braccio di Rv rispetto ad O centro di rotazione;
ogni termine risulta funzione di t dove t è la profondità del centro di rotazione rispetto al piano di riferimento di valle (piano campagna a valle). La lunghezza necessaria per assicurare l'equilibrio alla traslazione orizzontale si ottiene aumentando t come segue:
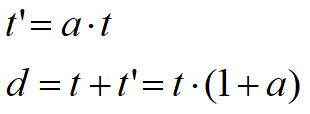
dove a = 0.2 (Metodo di Blum)
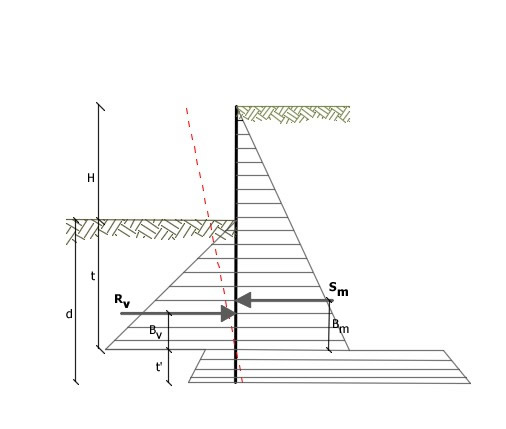
Schema di riferimento per il calcolo dell'equilibrio della paratia
Coefficiente di sicurezza sulla resistenza passiva
La lunghezza d’infissione d come sopra determinata è relativa alla condizione limite di incipiente collasso, tramite un coefficiente F. E’ possibile introdurre un margine di sicurezza sulle resistenze passive; la riduzione si effettua come segue:
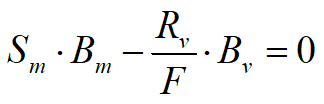
Paratia tirantata ad estremo libero
Calcolo della profondità d’infissione limite
La stabilità dell' opera è assicurata anche dai tiranti ancorati sulla paratia. Per utilizzare lo schema di calcolo ad estremo libero, la paratia deve essere sufficientemente corta e rigida. La lunghezza di infissione, sarà determinata imponendo l' equilibrio alla rotazione sull' origine del tirante indicato B1
![]()
Dove i simboli hanno il seguente significato:
Sm= componente orizzontale spinta attiva;
H= altezza terreno da sostenere;
t= profondità di infissione calcolata;
Bm= braccio di Sm rispetto alla base della paratia;
Pm= ordinata del punto di applicazione del tirante a monte;
Rv = componente orizzontale della resistenza passiva;
Bv = braccio di Rv.
Noto t, si determinano Sm ed Rv ed il relativo sforzo del tirante.
Coefficiente di sicurezza F sulle resistenze passive
La lunghezza d’infissione sarà ulteriormente aumentata per avere margine di sicurezza in condizioni di esercizio tramite il coefficiente di sicurezza F:
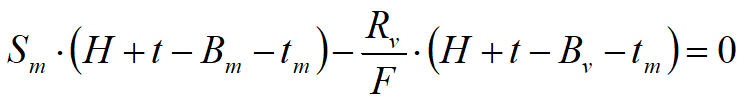
Paratia tirantata ad estremo fisso
Calcolo della profondità d’infissione limite
Se la sezione più profonda della paratia non trasla e non ruota può essere assimilata ad un incastro, in tal caso la paratia si definisce ad estremo fisso. Un procedimento elaborato da BLUM consente di ricavare la profondità d’infissione (t+t'), imponendo le condizioni cinematiche di spostamenti nulli alla base dell' opera ed all' origine del tirante (B1), e le condizioni statiche di momento e taglio nullo alla base della paratia. Si perviene ad una equazione di 5° grado in (t+t') che può essere risolta in modo agevole.
Coefficiente di sicurezza F sulle resistenze
Per aumentare il fattore di sicurezza sono stati introdotti negli sviluppi numerici, valori delle resistenze passive ridotte.
© GeoStru