Termenul de filtrare se referă la fenomenul fizic prin care apa trece dintr-o zonă cu o anumită energie într-o altă zonă cu o energie mai mică, printr-un mediu poros. Energia poate fi exprimată ca sumă a energiei cinetice legate de viteza fluidului, a energiei potențiale care depinde de poziția punctului și a energiei de presiune a lichidului în același punct. Deoarece viteza de filtrare este întotdeauna foarte mică, termenul cinetic este neglijabil. La studiul filtrării apei pot apărea probleme, atât de mișcare permanentă, cât și de mișcare variabilă. În ceea ce privește presiunea apei, care joacă un rol important în majoritatea problemelor de stabilitate, trebuie reținut faptul că, în cazul mișcării permanente, aceasta rămâne constantă în timp, în timp ce în cazul mișcării variabile este o funcție a timpului și, prin urmare, poate crește sau scădea odată cu acesta. Referitor la cantitatea de apă care trece printr-o anumită zonă în fenomenul de filtrare, trebuie amintit că în regim permanent cantitatea de apă care intră este egală cu cantitatea de apă care iese, în timp ce în regim variat nu există egalitate, iar diferența reprezintă volumul de apă acumulat sau expulzat din sol în intervalul de timp considerat. În fenomenul de consolidare, care este o condiție particulară a regimului variat, intră în joc și compresibilitatea solului.În regim permanent, zona de sol în care are loc filtrarea, în schema de reprezentare pe care o adoptăm, are două tipuri de limite: unul este locul în care se cunoaște sarcina de apă și este definit ca limită sau condiție limită a potențialului; celălalt este o margine de materiale impermeabile, cum ar fi rocile impermeabile, argilele etc., care delimitează stratul în care are loc filtrarea și este definit, prin urmare, ca limită sau condiție limită a fluxului de apă. Pentru a clarifica acest lucru, este suficient să ne amintim, de exemplu, condițiile de curgere a apei în testul de permeabilitate cu sarcină constantă. În acest încercare, bineînțeles, limitele potențiale sunt suprafețele de intrare și de ieșire a apei din eșantionul de pământ. Deoarece pereții recipientului sunt impermeabili, fluxul este paralel cu recipientul, iar peretele formează limita fluxului de apă:
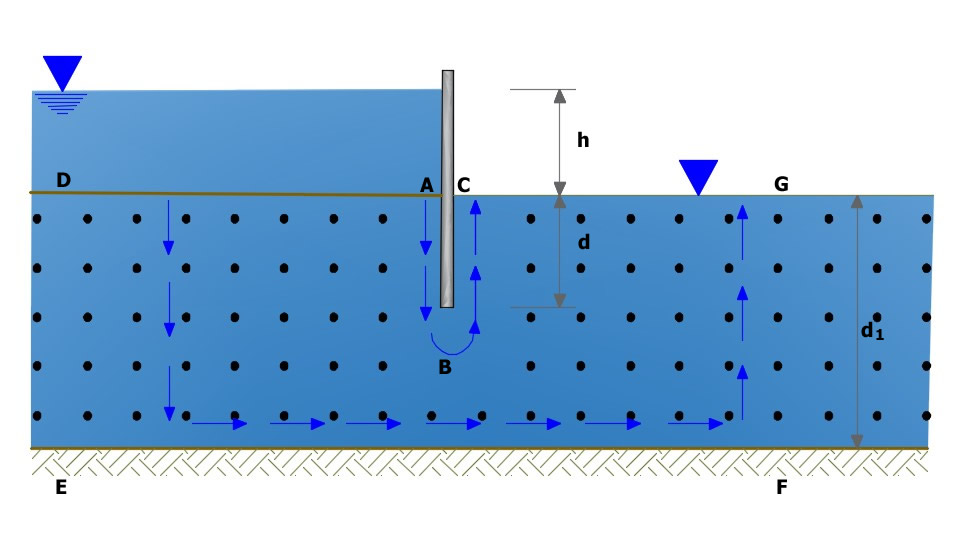
Schema relativă fluxului de apă
Un caz practic este cel al palplanșei (figura de mai sus) care susține un nivel constant h de apă și care este înfiptă în pământ la o adâncime d într-un strat omogen de sol permeabil (nisip sau pietriș) de grosime dI, care se sprijină pe un strat impermeabil (rocă sau argilă). În acest caz, există o mișcare confinată, deoarece condițiile de margine a regiunii în care are loc mișcarea sunt definite geometric. Fluxul de apă este cauzat de sarcina hidraulică h; pe suprafața AD acționează o sarcină constantă și această suprafață constituie prima limită a potențialului din problema noastră; pe CG sarcina este de asemenea constantă și această suprafață constituie a doua limită. În mod evident, pentru a-și îndeplini sarcinile, palplanșeta trebuie să fie impermeabilă, astfel încât suprafața sa ABC constituie una dintre limitele de curgere, în timp ce suprafața EF a stratului impermeabil va constitui cealaltă limită. Evident, din punct de vedere teoretic, dacă caracteristicile apei, ale solului și ale stratului impermeabil, în amonte și în aval de palplanșe, rămân constante, se poate considera că punctele D, E, F și G se află la infinit; în practică, se consideră în general că se află la o distanță de 4-5 ori grosimea stratului. Pentru a determina cantitatea de apă care se infiltrează în teren, se face ipoteza că fluxul de apă este guvernat de legea lui Darcy și că solul este omogen, izotrop și incompresibil:
![]()
Trebuie reamintit faptul că legea lui Darcy este valabilă pentru mișcarea laminară, condiție care apare pentru anumite valori ale numărului Reynolds, R. Valoarea lui R, care caracterizează trecerea de la mișcarea laminară la cea turbulentă, ia valori diferite în funcție de autori; Taylor (1948) a indicat R <= 1 ca fiind un criteriu de validitate pentru legea lui Darcy. Alți cercetători au examinat, în special pentru argile, legătura dintre condițiile de mișcare și gradientul hidraulic; în special Tavenas și alți (1983) au ajuns la concluzia că, pentru argile, legea lui Darcy este valabilă pentru gradienți între 0,1 și 50. Pentru a calcula capacitatea de curgere prin soluri, este util să se determine distribuția presiunii apei din pori prin construirea grilei de curgere, adică sistemul de linii de curent și linii echipotențiale care reprezintă fluxul apei printr-un sol incompresibil. Acceptând ipoteza unui sol incompresibil pentru mișcările de filtrare în regim permanent și plan, ecuația de continuitate poate fi scrisă sub forma:
![]()
Cele două componente ale vitezei lichidului, în conformitate cu legea lui Darcy, pot fi exprimate sub forma:
![]()
![]()
Combinând aceste trei ecuații se obține:
![]()
care este ecuația Laplace pentru mișcarea permanentă într-un plan, presupunând un material omogen, izotrop și incompresibil. Această ecuație poate fi exprimată prin intermediul a două funcții conjugate φ și ψ. De fapt, putem exprima componentele vitezei ca derivate parțiale în raport cu x și z ale funcției φ = k h și astfel:
![]()
![]()
Atunci se poate scrie și:
![]()
Existența funcției φ = k h, o funcție potențială de viteză pentru un fluid în mișcare, implică o vorticitate nulă și că mișcarea este irrotațională. Putem spune atunci că avem o funcție de curent astfel încât:
![]()
Așadar, avem:
![]()
![]()
De asemenea, putem scrie:
![]()
φ și ψ sunt cunoscute ca funcție de potențial și, respectiv, funcție de curent. Dacă luăm acum cazul, indicat mai devreme, al apei care se infiltrează prin sol sub o palplanșă (figura de mai jos), avem că două linii echipotențiale sunt suprafețele solului în amonte și în aval de palplanșa însăși; în plus, suprafața stratului impermeabil este o linie de curent sau de flux. Rezolvând ecuația Laplace în conformitate cu aceste condiții la limită, putem construi rețeaua de curgere. Fiecare fâșie dintre două linii de curgere adiacente este un canal de curgere, iar fiecare parte a canalului de curgere dintre două linii echipotențiale este un câmp. Prin urmare, este convenabil să se construiască liniile echipotențiale astfel încât diferența de înălțime piezometrică între două linii succesive să fie constantă, iar liniile de curgere astfel încât fiecare canal de curgere să fie constant. Dacă h este sarcina hidraulică totală și Na este numărul de gradienți piezometrici identificați, diferența de sarcină hidraulică între două linii echipotențiale succesive este:
![]()
La un punct z, așa cum se arată în figura următoare, presiunea se menține:
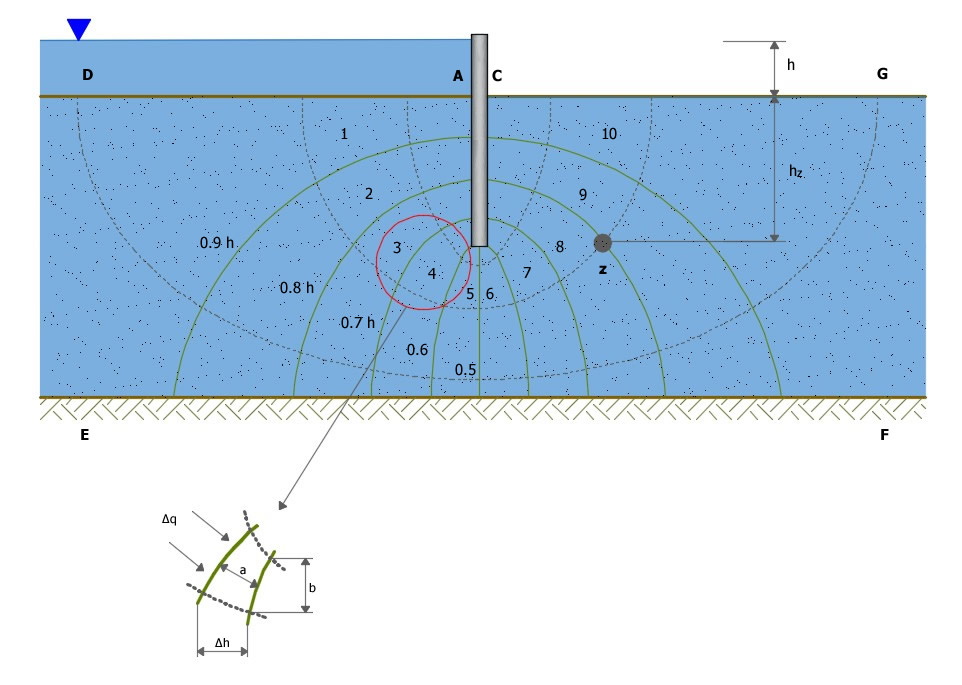
Schematizarea rețelei de curgere
n fiind numărul de gradienți piezometrici traversați pentru a ajunge la z. În exemplul din figura de mai sus avem:
![]()
Dacă nu ar exista niciun flux de apă, adică dacă suprafața din aval ar fi impermeabilă, presiunea hidrostatică în acest punct ar fi de valoare:
![]()
Deoarece apa este în mișcare, există o cădere de presiune, care, conform rețelei de filtrare trasate în punctul z, este de 8/10h. Prin urmare, suprapresiunea apei în punctul z este dată de:
![]()
Pentru a cunoaște capacitatea de filtrare considerăm un câmp, adică o zonă cuprinsă între două linii de curgere și două linii echipotențiale; lungimea laturii în direcția liniilor de curgere este a și, prin urmare, gradientul hidraulic într-un câmp este::
![]()
și viteza:
![]()
Să presupunem că cealaltă latură a câmpului are lungimea b, atunci capacitatea prin câmp pe unitatea de lungime a palplanșei va fi:
![]()
pentru fiecare tub de curgere; dacă b = a, adică dacă elementele rețelei de filtrare sunt pătrate, se obține:
![]()
Dacă Nb este numărul total de canale de curgere, capacitatea totală pe unitatea de lungime a palplanșei va fi:
![]()
Astfel, când rețeaua de filtrare a fost construită, capacitatea poate fi calculat cu ușurință. Rețeaua de filtrare este adesea construită prin metode experimentale în laborator, cu modele analogice sau grafice prin încercări. În situații complexe de subsol, datorită succesiunii straturilor și a anizotropiei permeabilității, rețeaua de filtrare poate fi obținută cu ajutorul metodelor numerice (FEM, BEM, metoda diferențelor finite).
|
© GeoStru