Metoda elementelor finite este metoda care, mai mult decât oricare alta, se bazează pe fundamente teoretice solide și raționale. De fapt, întreaga metodă presupune că problema este abordată ținând cont atât de aspectul static (și deci de echilibrul problemei), cât și de aspectul cinematic (și deci de congruența deplasărilor sau mai degrabă a deformațiilor). În metoda FEM, peretele de susținere este modelat ca un set de grinzi (elemente BEAM), cu constrângere de continuitate față de sol prin intermediul unor arcuri elastice, a căror rigiditate este evaluată în funcție de proprietățile elastice ale solului. Figura următoare prezintă schematic modelul utilizat pentru analiza cu elemente finite:
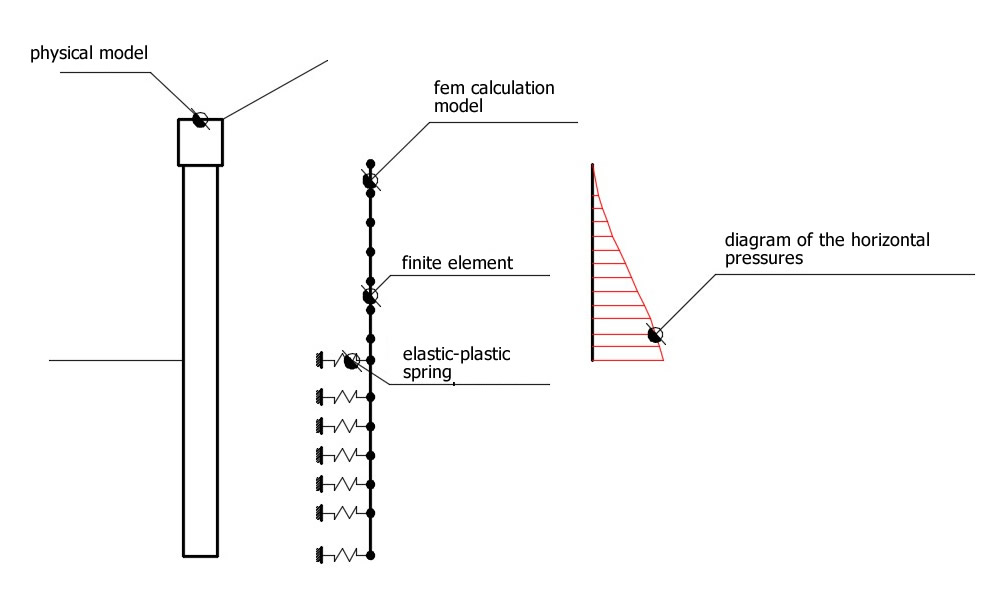
Schematizarea complexului pereți de susținere-teren cu ajutorul elementelor finite
Metoda elementelor finite necesită cunoașterea proprietăților solului și ale structurii (spre deosebire de metoda LEM, în care se impune o condiție de echilibru a corpului rigid). În special, este necesar să se cunoască modulul de reacție al solului. Principalele părți ale aplicării metodei sunt următoarele:
Caracterizarea materialelor și a structurii prin
▪ evaluarea coeficienților de împingere activi și pasivi, precum și a modulului de reacție pentru sol
▪ evaluarea rigidității la încovoiere, la forfecare și normală a peretelui de susținere;
▪ discretizarea peretelui de susținere în elemente finite și modelarea arcurilor:
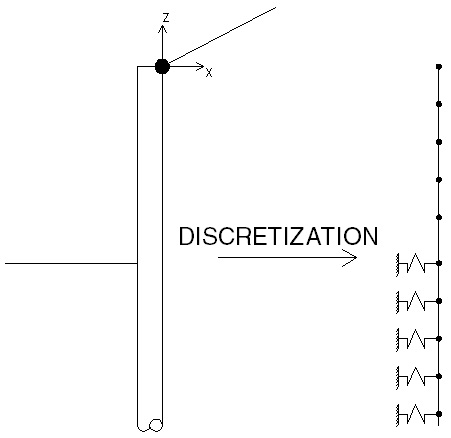
Procedura de discretizare
- Asamblarea contribuțiilor elementelor finite individuale
În această etapă, problema este readusă la nivel global, asamblându-se contribuțiile de rigiditate ale elementelor finite individuale.
- Soluția problemei
Problema cu elemente finite se pune în termenii unui sistem neliniar în variabilele de deplasare. În această etapă, se stabilește o procedură iterativă pentru a rezolva o problemă neliniară de tipul:
![]()
În ecuația de mai sus, K(u) este matricea de rigiditate a problemei (de tip neliniar), u este câmpul de deplasare care reprezintă soluția problemei, iar p este vectorul de sarcini externe (vectorul asociat cu distribuția presiunilor din sol).
Asamblarea și interpretarea soluției
Odată ce valorile componentelor vectorului u au fost determinate, se pot obține toate informațiile (referitoare la analiza structurală). În special, se determină următoarele:
▪ Momentul;
▪ Forfecare;
▪ Efortul normal.
|
© GeoStru