La estimación de los asientos de la cimentación se efectúa de acuerdo a los criterios de la literatura para cimentaciones directas.
Particularmente, el cálculo se efectúa con el método de Berardi (1999). Tal método se puede aplicar tanto a depósitos normalmente consolidados como a depósitos sobreconsolidados. Este aspecto se toma en cuenta en la definición del módulo de Young en pequeñas deformaciones.
La aplicación del método de Berardi consiste en los siguientes pasos:
1)valoración del módulo de Young en pequeñas deformaciones (E’0) medio en el tracto de interés H referido a presiones efectivas igual a las geostáticas.
2)definición de la relación E’/E’0 y por tanto del módulo de Young “operativo” en función de la relación s/B con base en lo mostrado en la Figura 10 (s es el asiento y B e la dimensión de la cimentación).
3)definición de la curva presión-asiento con base en diferentes valores de s/B y de E’ y de la siguiente ecuación
![]()
q’n = (q’ – σ’v0) = incremento de presión efectiva promedio neta
q' = N/ A = presión efectiva ejercitada sobre el terreno por la cimentación en kPa
N = carga vertical que comprende el peso efectivo de la cimentación aislada
A = área de la cimentación
σ'v0 = presión vertical efectiva geostática en la cota de intradós cimentación aislada
B = dimensión menor de la cimentación
ν' = relación de Poisson
Is = coeficiente de influencia (véase la Tabla 3 a continuación)
4) Estimación del asiento entrando en la curva del punto anterior con el valor de proyecto de q’n .
El espesor de la zona compresible Hc se asume, conservadoramente, como a continuación:
- cimentaciones cuadradas o circulares: Hc = 2·B
- cimentaciones continuas (L/B>10): Hc = 3,5·B
- cimentaciones rectangulares (L/B<10): Hc variable linealmente entre 2·B e 3,5·B.
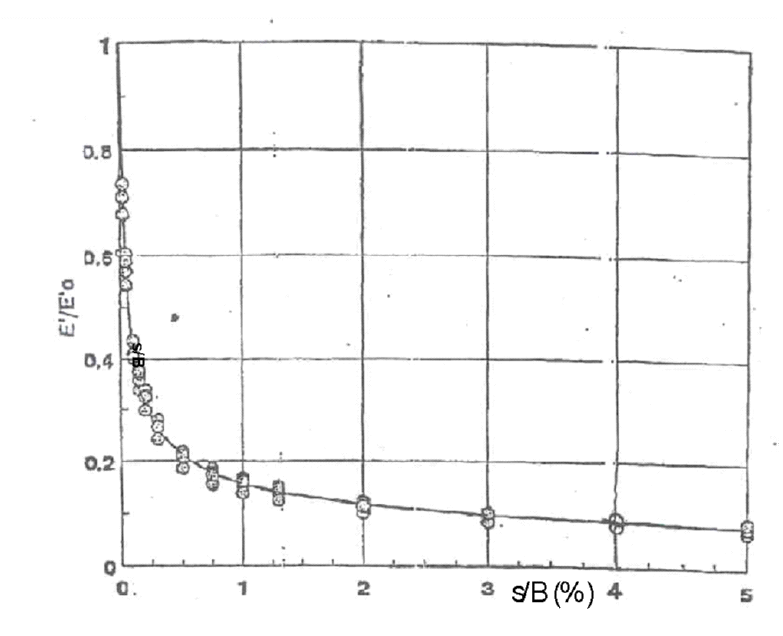
Figura 10. Curva de caída del módulo de Young en función de s/B (Berardi, 1999)
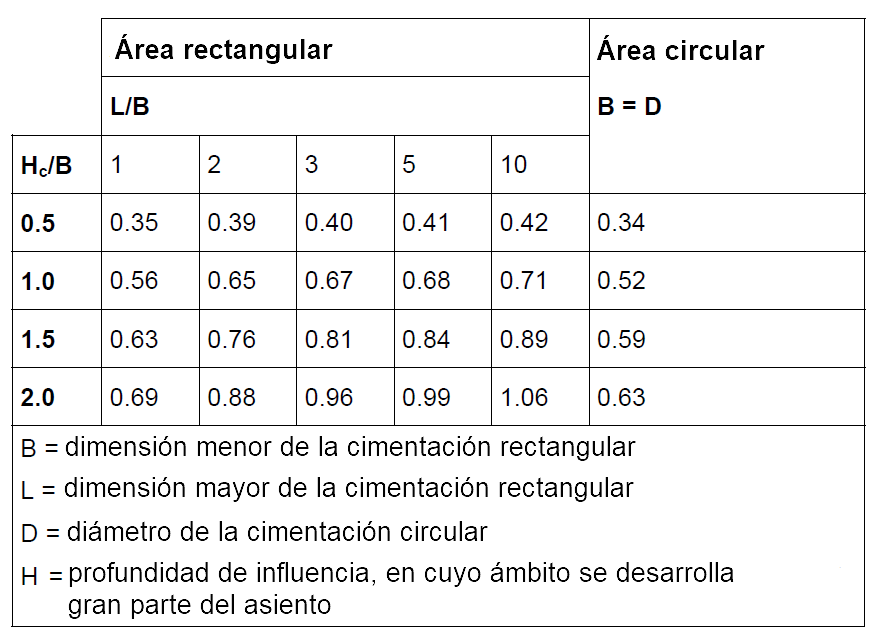
Tabla 3. Valores del coeficiente de influencia Is (Tsytovich, 1951)
© GeoStru