La valutazione dei cedimenti della fondazione è stata effettuata in accordo ai criteri di letteratura per fondazioni dirette.
In particolare, il calcolo è stato condotto con il metodo di Berardi (1999). Tale metodo può essere applicato sia a depositi normalmente consolidati che a depositi sovraconsolidati, essendo tale aspetto tenuto in conto nella definizione del modulo di Young a piccole deformazioni.
L’applicazione del metodo di Berardi consiste nei seguenti passi:
1)valutazione del modulo di Young a piccole deformazioni (E’0) medio nel tratto di interesse H riferito a pressioni efficaci pari a quelle geostatiche.
2)definizione del rapporto E’/E’0 e quindi del modulo di Young “operativo” in funzione del rapporto s/B sulla base di quanto riportato nella Figura 10 (s è il cedimento e B è la dimensione della fondazione).
3)definizione della curva pressione-cedimento sulla base di diversi valori di s/B e di E’ e della seguente equazione:
![]()
q’n = (q’ – σ’v0) = incremento di pressione efficace media netta
q' = N/ A = pressione efficace esercitata sul terreno dalla fondazione in kPa
N = carico verticale comprensivo del peso efficace del plinto
A = area della fondazione
σ'v0 = pressione verticale efficace geostatica alla quota intradosso plinto
B = dimensione minore della fondazione
ν' = rapporto di Poisson
Is = coefficiente di influenza (vedi la Tabella 3 seguente)
4) valutazione del cedimento entrando nella curva di cui al punto precedente con il valore di progetto di q’n .
Lo spessore della zona compressibile Hc è stato ipotizzato cautelativamente come segue:
- fondazioni quadrate o circolari: Hc = 2·B
- fondazioni nastriformi (L/B>10): Hc = 3,5·B
- fondazioni rettangolari (L/B<10): Hc variabile linearmente tra 2·B e 3,5·B.
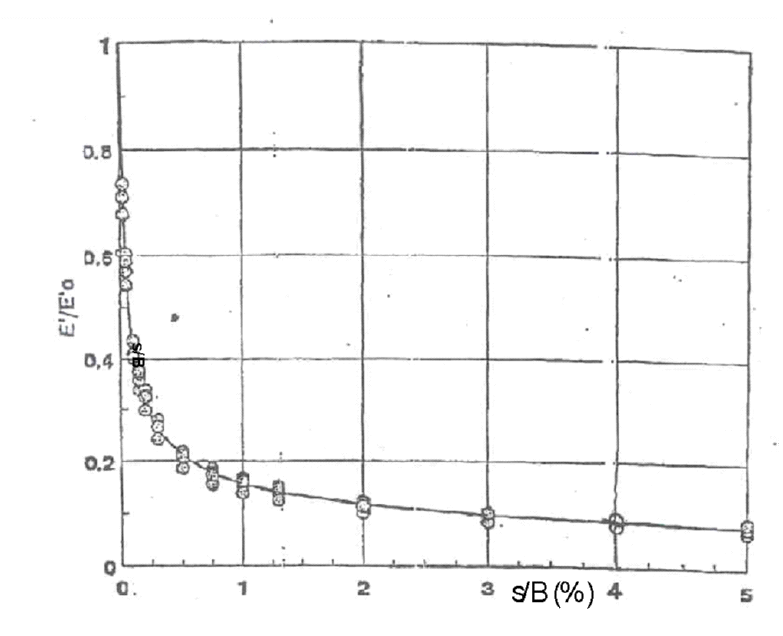
Figura 10. Curva di decadimento del modulo di Young in funzione di s/B (Berardi, 1999)

Tabella 3. Valori del coefficiente di influenza Is (Tsytovich, 1951)
© GeoStru