SARCINA LIMITĂ A RADIERULUI
Sarcina limită a unei fundații de suprafață poate fi definită cu referire la acea valoare de încarcare maximă pentru care condiția de rupere nu este atinsă în niciun punct din subsol (metoda Frolich); Sau prin referire la acea valoare de sarcină, mai mare decât cea anterioară, pentru care fenomenul de ruptură s-a extins la un volum mare de sol (metoda Prandtl și cele ulterioare).
Prandtl a studiat problema rupturii unui semi-spațiu elastic datorită unei sarcini aplicate pe suprafața sa cu referire la oțel, caracterizând rezistența la rupere cu o lege de tip:
τ = c+σ∙tanφ valabilă și pentru soluri
Ipotezele și condițiile introduse de Prandtl sunt următoarele:
- Material fără greutate și, prin urmare, γ = 0.
- Comportament rigid - plastic.
- Rezistența la rupere a materialului exprimată de relația: τ = c+σ∙tanφ
- Sarcină uniformă, verticală și aplicată pe o bandă de lungime infinită și lățime 2b (stare de deformare plată).
- Zero solicitări tangențiale la contactul dintre suprafața de încărcare și suprafața de delimitare a semi-spațiului.
În momentul rupturii, se produce plastifierea materialului închis între suprafața de delimitare a semi-spațiului și suprafața GFBCD (vezi fig. 2).
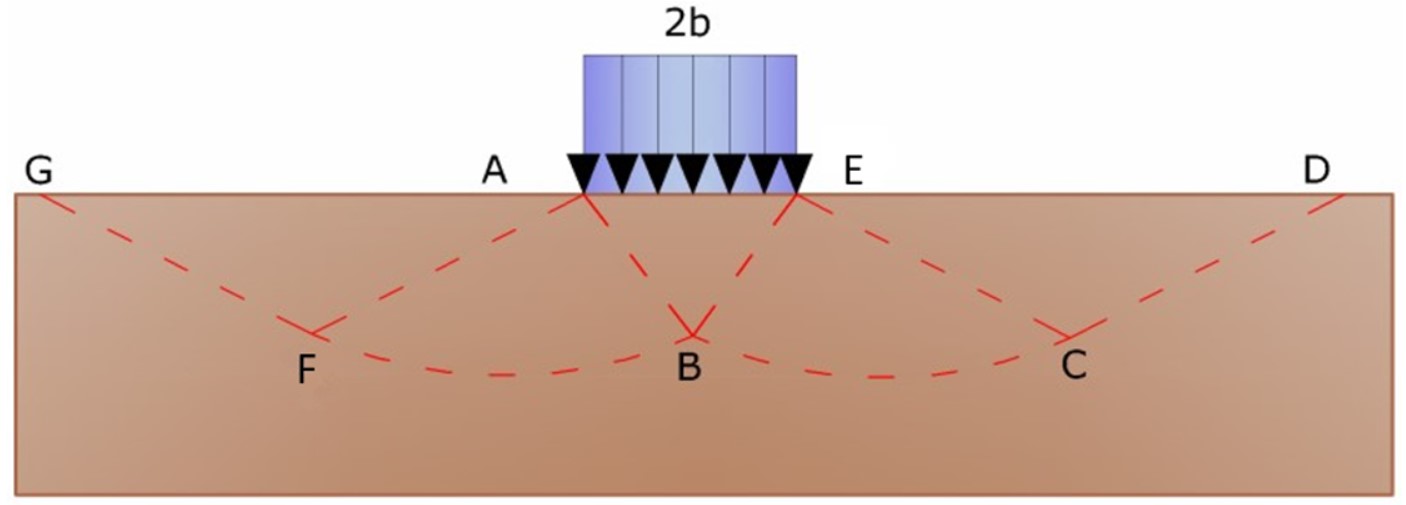
Figura 2. - Mecanismul de rupere Prandtl
Astfel, odată ce a fost identificat volumul de sol adus la rupere de sarcina limită, acest lucru poate fi calculat prin scrierea condiției de echilibru între forțele care acționează asupra oricărui volum de sol delimitat în partea de jos de oricare dintre suprafețele de alunecare.
Aceasta conduce la o ecuație q =B∙c, unde coeficientul B depinde doar de unghiul de frecare φ al solului.
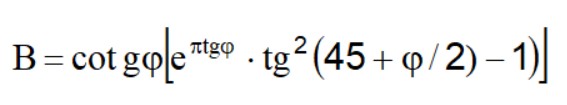
Pentru φ =0 coeficientul B este egal cu 5.14, deci q=5.14∙c.
În celălalt caz particular al solului fără coeziune (c=0, γ≠0) rezultă q = 0, conform teoriei lui Prandtl, prin urmare nu ar fi posibilă aplicarea nici unei sarcini pe suprafața limită a unui sol necoeziv.
Această teorie, deși, practic nu este aplicabilă, a dat naștere tuturor metodelor de cercetare și de calcul ulterioare.
De fapt, Caquot a fost, în aceleași condiții ca și Prandtl, cu excepția faptului că fâșia de încărcare nu mai este aplicată pe suprafața limită a semi-spațiului, ci la o adâncime h, cu h ≤ 2b; solul dintre suprafață și adâncimea h are următoarele caracteristici: γ≠0, φ =0, c=0, reprezintă un mijloc dotat cu greutate, dar fără rezistență.
Rezolvând ecuațiile de echilibru ajungem la expresia:
q=A∙γ1 + B∙c
care este cu siguranță cu un pas înainte față de Prandtl, dar care, încă nu reflectă realitatea.
Metoda lui Terzaghi (1955)
Terzaghi, continuând studiul lui Caquot, a făcut unele modificări pentru a lua în considerare caracteristicile reale ale întregii lucrări de fundație-sol.
Sub acțiunea sarcinii transmise de fundație, solul, care este în contact cu fundația tinde să refuleze lateral, dar este împiedicat de rezistențele tangențiale care se dezvoltă între fundație și sol. Aceasta implică o modificare a stării de solicitare în solul situat direct sub fundație; Pentru a lua în considerare acest lucru, Terzaghi atribuie laturilor AB și EB ale penei Prandtl o înclinație y față de orizontală, alegând valoarea lui y în funcție de caracteristicile mecanice ale solului la contactul sol-fundație.
Ipoteza g2 = 0 pentru solul aflat sub fundație este astfel depășită, presupunând că suprafețele de cedare (rupere) rămân neschimbate, expresia sarcinii limită este, prin urmare:
q = A∙γ1∙h + B∙c+C∙γ∙b
Unde C este un coeficient care rezultă în funcție de unghiul de frecare φ al solului de sub planul de referință și de unghiul φ definit mai sus; b este jumătatea lățimii fâșiei.
Mai mult, pe baza datelor experimentale, Terzaghi trece de la problema planului la problema spațială prin introducerea factorilor de formă.
Terzaghi a adus o contribuție suplimentară la comportamentul real al solului.
În metoda Prandtl se presupune un comportament rigid-plastic al solului, în schimb, Terzaghi admite acest comportament în soluri foarte compacte. În acestea, de fapt, curba de sarcini-tasări are o primă secțiune dreaptă, urmată de o secțiune scurtă curbilinie (comportament elasto-plastic); cedarea ruperea) este instantanee și valoarea sarcinii limită este clar identificată (cedarea generală).
Pe de altă parte, într-un teren foarte slab, relația sarcină-tasare prezintă o secțiune curbilinie care se accentuează de la cele mai mici sarcini, ca urmare a unei ruperi progresive în sol (ruptură locală); prin urmare, identificarea sarcinii limită nu este la fel de clară și evidentă ca în cazul solurilor compacte.
Explicând coeficienții formulei anterioare, formula lui Terzaghi poate fi scrisă:
q = c∙Nc∙sc+γ∙D∙Nq+0.5∙γ∙B∙Nγ∙sγ
Unde:
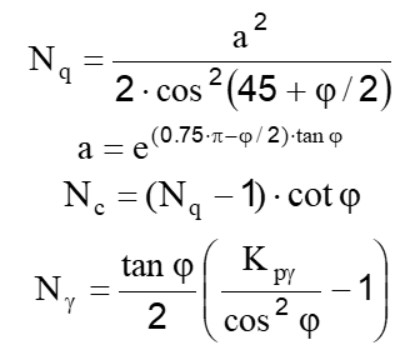
Cu:

Formula lui Meyerhof (1963)
Meyerhof a propus o formulă pentru calcularea sarcinii limită similară cu cea a lui Terzaghi; diferențele constau în introducerea unor coeficienți de formă suplimentari.
El a introdus un coeficient sq care multiplică factorul Nq, factorii de adâncime și panta ii, în cazul în care sarcina transmisă fundației este înclinată pe verticală.
Valorile coeficienților N au fost obținute de Meyerhof presupunând diverse arcuri de test BD (v. Mecanismul Prandtl), având în vedere valorile aproximative ale forfecării care se dezvoltă în sol deasupra planului de referință. Factorii de formă luați de la Meyerhof sunt prezentați mai jos, împreună cu expresia formulei.
q = c∙Nc∙sc∙dc + γ∙D∙Nq∙dq + 0.5∙γ∙B∙Nγ∙sγ∙dγ
Unde:

Formula lui Hansen (1970)
Este o extensie suplimentară a formulei lui Meyerhof; extensiile constau în introducerea unor termeni pentru a lua în considerare înclinația fundației și introducerea fundației într-o pantă.
Formula lui Hansen este valabilă pentru orice raport D/B, prin urmare, atât pentru fundații superficiale, același autor a introdus coeficienți pentru a interpreta mai bine comportamentul real al fundației, fără aceștia, de fapt, ar exista o creștere prea puternică a sarcinii limită cu adâncime.
Factori de adâncime
Pentru valorile D/B<1:
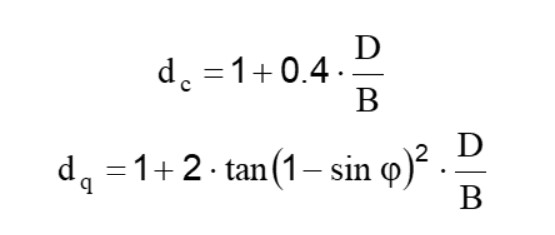
Pentru valorile D/B>1:
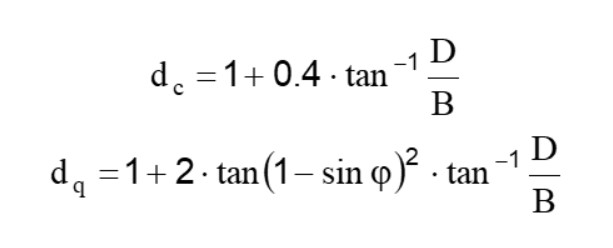
În cazul φ=0

Factori de formă

Factori de înclinare a solului (fundație pe un versant înclinat)
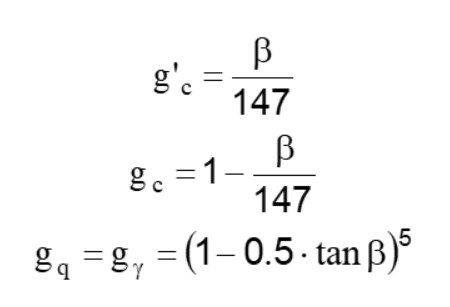
În următorii factori, expresiile cu ghilimele (') se aplică atunci când φ = 0.
Formula lui Vesic (1975)
Formula lui Vesic este analogă cu formula lui Hansen, cu Nq și Nc ca pentru formula lui Meyerhof și cu Ng după cum se arată mai jos:
![]()
Factorii de formă și adâncime care apar în formulele de calcul ale capacității portante sunt aceiași cu cei propuși de Hansen; unele diferențe sunt raportate în schimb la factorii de înclinare a terenului (fundație pe un versant).
TASĂRI ELASTICE
Tasările unei fundații dreptunghiulare de dimensiuni BxL plasate pe suprafața unui semi-spațiu elastic pot fi calculate pe baza unei ecuații bazate pe teoria elasticității (Timoshenko și Goodier, 1951):
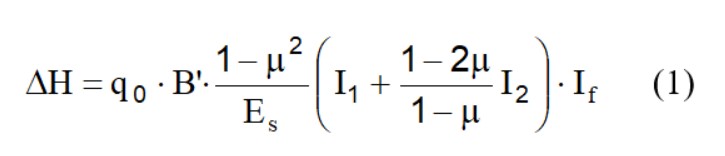
Unde:
q0 Intensitatea presiunii de contact
B' Dimensiunea minimă a suprafeței reactive;
E e m Parametrii elastici ai solului.
Ii Coeficienții ei influență funcție de: L'/B', grosimea stratului H, coeficientul lui Poisson
m, adâncimea suprafeței de referință D.
Coeficienții I1 și I2 pot fi calculați utilizând ecuațiile date de Steinbrenner (1934) (V. Bowles), în funcție de raportul L'/B' și H/B, folosind B'=B/2 și L'=L/2 pentru coeficienții relativi la centru și B'=B și L'=L pentru coeficienții relativi marginii.
Coeficientul de influență IF este derivat din ecuațiile Fox (1948), care indică faptul că tasarea se reduce în funcție de adâncime în funcție de coeficientul lui Poisson și a raportului L/B.
Pentru a simplifica ecuația (1) se introduce coeficientul IS:
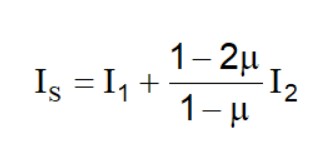
Tasarea stratului de grosime H este:
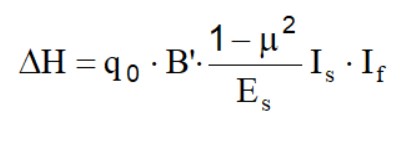
Pentru o mai bună aproximare a tasărilor, baza de spijin este împărțită astfel încât punctul să fie plasat la un colț extern, comun mai multor dreptunghiuri. În practică, aceasta se înmulțește cu un factor egal cu 4 pentru calcularea tasărilor din centru și cu un factor egal cu 1 pentru tasările la margine. La calculul tasărilor, se ia în considerare o adâncime a bulbului de tensiuni egală de 5B, dacă roca de bază (substratul stâncos) este la o adâncime mai mare. În acest sens, roca de bază este considerat a fi un strat cu o valoare E de 10 ori mai mare decât stratul de mai sus. Modulul elastic pentru solurile stratificate se calculează ca media ponderată a modulelor elastice ale straturilor afectate de tasări imediate.
© GeoStru