ÎNCERCĂRI DE PENERTOMETRIE DINAMICE CONTINUE
(DYNAMIC PROBING)
DPL-DPM–DPH-DPSH
Note ilustrative - Diverse tipologii de penetrometre dinamice
Încercarea de penetrometrie dinamică constă în introducerea în teren a unui vârf conic (înaintări progresive δ) măsurând numărul de lovituri N necesar.
Încercările de Penetrometrie Dinamice sunt foarte răspândite și utilizate de către geologi și geotehniști, datorită simplității executive, rentabilității și vitezei de execuție.
Elaborarea, interpretarea și vizualizarea grafică a acestora permite “catalogarea și parametrizarea” solului parcurs cu ajutorul unei imagini continue, care permite o comparație între consistența diverselor nivele traversate și o corelație directă cu sondajele geognostice pentru caracterizarea stratigrafică.
Sonda penetrometrică permite de asemenea recunoașterea destul de precisă a grosimii păturilor din substrat, cota eventualelor nivele freatice, suprafețe de ruptură în taluzuri și consistența generală a terenului.
Utilizând datele deduse din corelațiile indirecte și făcând referire la diverși autori, trebuie să fie tratată cu precauția corespunzătoare și, dacă este posibil, după experiența geologică dobândită pe teren.1
Elemente caracteristice ale penetrometrului dinamic sunt următoarele:
- greutate ciocan M;
- înălțime liberă cădere H;
- vârf conic: diametru bază con D, suprafața bazei A (unghi de deschidere α);
- avansare (penetrare) δ;
- prezența/absența cămășuirii externe (noroi bentonitic).
În ceea ce privește clasificarea ISSMFE (1988) diverselor tipuri de penetrometre dinamice (vezi tabelul de mai jos) există o subdiviziune inițială în patru clase (pe baza greutății M a ciocanului):
- tip UȘOR (DPL);
- tip MEDIU (DPM);
- tip GREU (DPH);
- tip SUPERGREU (DPSH);
Clasificarea ISSMFE a penetrometrelor dinamice:
Tip |
Acronime |
Greutate ciocan M (kg) |
Adâncime maximă probă (m) |
Ușor |
DPL (Uşor) |
M ≤ 10 |
8 |
Mediu |
DPM (Mediu) |
10 < M < 40 |
20-25 |
Greu |
DPH (Greu) |
40 ≤ M < 60 |
25 |
Super-greu(Super Heavy) |
DPSH |
M ≥ 60 |
25 |
1 În funcție de tipul probei, și alegerea caracterizării naturii terenurilor investigate (necoezive/coezive, coezive/necoezive - teren cu un comportament intermediar, care nu poate fi încadrat în mod cert), este făcută sub îndrumarea profesionistului (geologului) desemnat în funcție de competența și de experiența în zonă.
Penetrometre utilizate în Italia
În Italia sunt utilizate următoarele tipuri de penetrometre dinamice (care însă nu au intrat în standardul ISSMFE):
•DINAMIC UȘOR (DL-30) (MEDIU conform clasificării ISSMFE)
ciocan M = 30 kg, înălțime de cădere H = 0.20 m, penetrare δ = 10 cm, vârf conic (α=60-90°), diametru D 35.7 mm, aria bazei conului A=10 cm² cămășuire /noroi bentonitic: prevăzut;
•DINAMIC UȘOR (DL-20) (MEDIU conform clasificării ISSMFE)
ciocan M = 20 kg, înălțime de cădere H=0.20 m, penetrare δ = 10 cm, vârf conic (α= 60-90°), diametru D 35.7 mm, aria bazei conului A=10 cm² cămășuire /noroi bentonitic: prevăzut;
•DINAMIC GREU (SUPERGREU conform clasificării ISSMFE)
ciocan M = 73 kg, înălțime de cădere H=0.75 m, penetrare δ=30 cm, vârf conic (α = 60°), diametru D = 50.8 mm, aria bazei conului A=20.27 cm² cămășuire: prevăzută în funcție de indicații precise;
•DINAMIC SUPERGREU (Tip EMILIA)
ciocan M=63.5 kg, înălțime de cădere H=0.75 m, penetrare δ=20-30 cm, vârf conic (α = 60°-90°) diametru D = 50.5 mm, aria bazei conului A = 20 cm², cămășuire /noroi bentonitic: prevăzut.
CORELAȚIE CU NSPT
Deși încercarea de penetrometrie standard (SPT) reprezintă azi unul dintre mijloacele cele mai răspândite și economice pentru obținerea de informații din subsol, marea parte a corelațiilor existente privesc numărul de lovituri NSPT obținut cu ajutorul încercării, este necesară raportarea numărului de lovituri al unei încercări dinamice cu NSPT. Transformarea este dată de:
NSPT = βT * N
Unde:
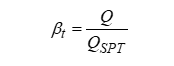
în care Q reprezintă energia specifică pentru lovitură și QSPT reprezintă energia care se referă la încercarea SPT.
Energia specifică pentru lovitură se calculează în acest mod:
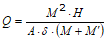
în care
M greutate ciocan;
M’ greutate prăjini;
H înălțime cădere;
A suprafața laterală a conului;
δ intervalul de penetrare.
Evaluarea rezistenței dinamice a conului RPD
Formula Olandeză
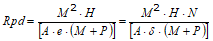
Rpd rezistența dinamică a conului (arie A).
e penetrare medie pe lovitură (pas instrument împărțit la număr lovituri) (δ/N).
M greutatea ciocanului (înălțimea de cădere H).
P greutate totală prăjini și sistem de lovire/batere.
Calculul (N1)60
(N1)60 este numărul de lovituri normalizat definit ca:

ER/60 Randament sistem de foraj normalizat la 60%
Cs Parametru funcție de tub foraj (1.2 dacă lipsește).
Cd Funcție de diametrul forajului (1 dacă este cuprins între 65-115mm).
Cr Parametru de corecție funcție de lungimea prăjinilor.
Metodologie de Prelucrare
Prelucrările au fost efectuate printr-un program de calcul automat Dynamic Probing produs de GeoStru.
Programul calculează raportul energiilor transmise (coeficientul de corelație cu SPT) prin elaborările propuse de către Pasqualini (1983) - Meyerhof (1956) - Desai (1968) - Borowczyk-Frankowsky (1981).
Permite de asemenea utilizarea datelor obținute din efectuarea încercărilor de penetrometrie pentru extrapolarea informațiilor geotehnice și geologice utile.
O vastă experientă dobândită, împreuna cu buna interpretare și corelare, permit obținerea datelor utile pentru proiectare, de multe ori date mai fiabile decât din alte surse bibliografice, aspra litologiilor precum și date geotehnice determinate asupra verticalelor litologice din puține încercări de laborator realizate ca și reprezentare generală a unei verticale eterogene neuniformă și/sau complexă.
În particular se obțin informații privind :
•evoluția vertical și orizontal al intervalelor stratigrafice;
•caracterizarea litologică a unităților stratigrafice;
•parametrii geotehnici sugerați de diverși autori în funcție de valorile numărului de lovituri și de rezistența pe con.
EVALUĂRI STATISTICE ȘI CORELAȚII
Prelucrarea Statistica
Permite prelucrarea statistică a datelor numerice din Dynamic Probing, utilizând în calcul valori reprezentative ale stratului, considerând o valoare inferioară sau superioară mediei aritmetice a stratului (valoare des utilizată);
valorile ce se pot introduce sunt :
Media
Media aritmetică a valorilor numărului de lovituri pe stratul considerat.
Media minimă
Valoarea statistică inferioară mediei aritmetice a valorilor numărului de lovituri pe stratul considerat.
Maxim
Valoarea maximă a valorilor numărului de lovituri pe stratul considerat.
Minim
Valoarea minimă a valorilor numărului de lovituri pe stratul considerat.
Deviația standard medie
Deviație standard medie a valorilor numărului de lovituri pe stratul considerat.
Media deviată
Valoarea statistică a mediei deviate a valorilor numărului de lovituri pe stratul considerat.
Media (+) deviație
Media + deviația (valoarea statistică) a valorilor numărului de lovituri pe stratul considerat.
Media (-) deviație
Media - deviația (valoarea statistică) a valorilor numărului de lovituri pe stratul considerat.
Distribuție normală R.C.
Valoarea lui Nspt,k este calculată pe baza unei distribuții normale sau gausiene, fixând o probabilitate de a nu depășii de 5%, conform relației de mai jos:
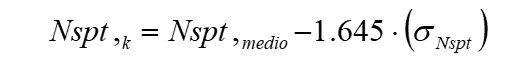
unde σNspt este deviația standard a lui Nspt.
Distribuție normală R.N.C.
Valoarea lui Nspt,k este calculată pe baza unei distribuții normale sau gausiene, fixând o probabilitate de a nu depășii de 5%, tratând valorile medii ale lui Nspt distribuite normal:
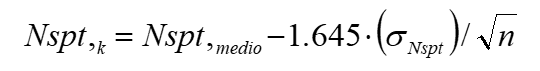
unde n este numărul de citiri.
Presiunea admisibilă
Presiunea admisibilă specifică pe interstrat (cu sau fără efect de reducere a energiei pentru mișcarea laterală a prăjinilor) calculată după cunoscutele elaborări propuse de Herminier, aplicând un coeficient de siguranță (în general = 20-22) care corespunde unui coeficient de siguranță standard pentru fundații egal cu 4, cu o geometrie standard cu lățime egală cu 1 m și adâncime d = 1m.
CORELAȚII GEOTEHNICE TERENURI NECOEZIVE
Lichefiere
Permite calculul potențialului de lichefiere al solurilor (în principal nisipoase) utilizând date NSPT.
Prin relația lui SHI-MING (1982), aplicabilă pentru terenuri nisipoase, lichefierea este posibilă numai dacă NSPT-ul stratului avut în vedere este inferior NSPT-ului critic conform prelucrării lui SHI-MING.
Corelație Nspt în prezența pânzei freatice
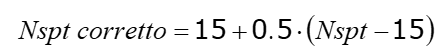
NSPT este valoarea medie în strat
corelația este aplicată în prezența pânzei freatice dacă numărul de lovituri este mai mare de 15 (corecția este realizată dacă pânza freatică se regăsește în întreg stratul).
Unghi de forfecare
•Peck-Hanson-Thornburn-Meyerhof (1956) - corelație validă pentru terenuri solide la adâncime < 5 m; corelația validă pentru nisipuri și pietrișuri reprezintă valori medii. corelație istorică foarte utilizată, valabilă pentru adâncime < 5 m pentru terenuri uscate și < 8 m pentru terenuri cu strat freatic (tensiuni < 8-10 t/mp).
•Meyerhof (1956) - corelație valabilă pentru terenuri argiloase și argiloase-marnoase fisurate, terenuri moi și pături detritice din modificarea experimentală a datelor).
•Sowers (1961) - Unghi de frecare în grade valid pentru nisipuri în general (cond. optime pentru adâncime < 4 m pentru terenuri uscate și < 7 m pentru terenuri cu strat freatic ) σ >5 t/mp.
•De Mello - corelație valabilă pentru terenuri predominant nisipoase și nisipoase-pietroase (din modificarea experimentală a datelor) cu unghiul de frecare < 38°.
•Malcev (1964) - Unghiul de frecare în grade valabil pentru nisipuri în general (cond. optime pentru adâncime > 2 m și pentru valorile unghiului de frecare < 38°).
•Schmertmann (1977) - Unghiul de frecare în grade pentru diversele tipuri litologice (valori maxime). N.B. valori de obicei prea optimiste, deduse din corelațiile indirecte din Dr (%).
•Shioi-Fukuni (1982) (ROAD BRIDGE SPECIFICATION) - Unghi de frecare în grade valabil pentru nisipuri - nisipuri fine sau prăfoase și prafuri (cond. optime pentru adâncimea încercării > 8 m terenuri uscate și > 15 m pentru terenuri cu strat freatic) σ>15 t/mp.
•Shioi-Fukuni (1982) (JAPANESE NATIONALE RAILWAY) - Unghi de frecare (grade) valabil pentru nisipuri medii, groșiere și cu pietriș.
•Owasaki & Iwasaki - Unghi de frecare în grade valabil pentru nisipuri - nisipuri medii, groșiere și cu pietriș (cond. optime pentru adâncimea > 8 m pentru terenuri uscate și > 15 m pentru terenuri cu strat freatic) σ >15 t/mp.
•Meyerhof (1965) – corelație valabilă pentru terenuri nisipoase cu % de praf < 5% cu o adâncime < 5 m și cu % de praf > 5% cu o adâncime < 3 m.
•Mitchell și Katti (1965) – corelație validă pentru nisipuri și pietrișuri.
Densitatea relativă (%)
•Gibbs & Holtz (1957) - corelație valabilă pentru orice presiune efectivă, pentru pietriș Dr este supraestimat, iar pentru prafuri subestimat.
•Skempton (1986) - elaborare valabilă pentru prafuri și nisipuri și nisipuri fine până la grosiere NC pentru orice presiune efectivă, pentru pietrișuri de valoarea Dr % este supraestimat, pentru prafuri este subestimat.
•Schultze & Menzenbach (1961) - pentru nisipuri fine și cu pietriș NC ,metodă valabilă pentru orice valoare de presiune efectivă în depozitele NC, pentru pietrișuri valoarea lui Dr % este supraestimată, pentru prafuri este subestimată.
Modulul lui Young [Ey (Kg/cmp)]
•Terzaghi - elaborare validă pentru nisip curat și pentru nisip cu pietriș fără să luăm în considerare presiunea efectivă.
•Schmertmann (1978) - elaborare valabilă pentru diferite tipuri litologice.
•Schultze-Menzenbach - elaborare valabilă pentru diferite tipuri litologice.
•D'Appollonia și alții (1970) - corelație validă pentru nisip, nisip SC, nisip NC și pietriș.
•Bowles (1982) - corelație validă pentru nisip argilos, nisip prăfos, nisip mediu, nisip, praf nisipos și pietriș.
Modul Edometric (Mo (Eed) (Kg/cmp))
•Begemann (1974) - elaborarea densității rezultată din încercări în Grecia corelație validă pentru praf cu nisip, nisip și pietriș.
•Buismann-Sanglerat - corelație valabilă pentru nisip și nisip argilos
•Farrent (1963) - corelație valabilă pentru nisip, nisip cu pietriș (din modificarea experimentală a datelor).
•Menzenbach și Malcev - corelație validă pentru nisipuri fine, nisipuri cu pietriș, nisip și pietriș.
Stare de consistență
•Clasificarea A.G.I. (1977)
Greutatea Volumică (t/mc)
•Meyerhof și alții, validă pentru nisipuri, pietrișuri, praf, praf nisipos.
Greutate Volumică Saturată
• Terzaghi-Peck (1948-1967)
Modulul lui poisson
•Clasificare A.G.I.
Potențial de lichefiere (Stress Ratio)
•Seed-Idriss (1978-1981) - Această corelație este validă numai pentru nisipuri, pietriș și prafuri nisipoase, reprezintă raportul dintre efortul dinamic mediu și tensiunea verticală de consolidare pentru calcularea potențialului de lichefiere a nisipurilor și terenurilor nisipoase cu pietriș prin intermediul graficelor autorilor.
Viteza undelor de forfecare Vs (m/s)
•Această corelație este validă numai pentru terenuri necoezive nisipoase și pietroase.
Modul dinamic de deformație (G)
•Ohsaki & Iwasaki - elaborare valabilă pentru nisipuri plastice și nisipuri curate.
•Robertson și Campanella (1983) și Imai & Tonouchi (1982) - elaborare validă mai ales pentru nisipuri și pentru tensiuni litostatice care se încadrează între 0,5 - 4,0 kg/cmp.
Modul de reacție (Ko)
•Navfac (1971-1982) - elaborarea validă pentru nisipuri, pietrișuri, praf, praf nisipos.
Rezisteță la vârf a penetrometrului static ( Qc (Kg/cmp))
•Robertson (1983) - Qc
CORELAȚII GEOTEHNICE PENTRU TERENURI COEZIVE
Coeziune nedrenată [Cu (Kg/cmp)]
•Benasși & Vannelli - corelații deduse din experiența firmei constructoare Penetrometre SUNDA 1983.
•Terzaghi-Peck (1948-1967) - corelație validă pentru argile nisipoase-prăfoase NC cu Nspt < 8, argile prăfoase cu plasticate medie, argile marnoase fisurate.
•Terzaghi-Peck (1948) - Cu (min-max).
•Sanglerat - din date Penetr. Static pentru terenuri coezive saturate, această de corelație nu este valabilă pentru argilele senzitive cu o sensibilitate > 5, pentru argile supraconsolidate fisurate și pentru prafuri cu plasticitate scăzută.
•Sanglerat - pentru argile prăfoase-nisipoase puțin coezive, valori valide pentru rezistențe penetrometrice < 10 lovituri, pentru rezistențe penetrometrice > 10 prelucrarea validă este aceea a "argilelor plastice" a lui Sanglerat.
•(U.S.D.M.S.M.) U.S. Design Manual Soil Mechanics - Coeziune nedrenată pentru argile prăfoase și argile cu plasticate medie și ridicată, (Cu-Nspt-grad de plasticitate).
•Schmertmann (1975) - (valori medii), valid pentru argile și nisipuri argiloase cu Nc=20 și Qc/Nspt=2.
•Schmertmann (1975) - (valori minime), validă pentru argile NC .
•Fletcher (1965) - (Argila de Chicago) Coeziune nedrenată, coloană valori valide pentru argile cu plasticitate medie-scăzută.
•Houston (1960) - argilă cu plasticitate medie-ridicată.
•Shioi-Fukuni (1982) , validă pentru terenuri puțin coezive și plastice, argilă cu plasticitate medie-ridicată.
•Begemann.
•De Beer.
Rezistența la vârf penetrometru static [Qc (Kg/cmp)]
• Robertson (1983) Qc.
Modul Edometric [Mo (Eed) (Kg/cmp)]
•Stroud și Butler (1975) - pentru litotipi cu plasticitate medie, valid pentru litotipi argiloși cu plasticitate medie - crescută - din experiențe pe argilele glaciare.
•Stroud și Butler (1975) - pentru litotipi cu plasticitate medie-scăzută (IP < 20), validă pentru litotipi argiloși cu plasticitate medie-scăzută (IP < 20) - din experiente pe argilele glaciare.
•Veșic (1970) - corelație validă pentru argile moi (valori minime și maxime).
•Trofimenkov (1974), Mitchell și Gardner - validă pentru litotipi argiloși și prăfoși-argiloși (raport Qc/Nspt=1.5-2.0).
•Buismann-Sanglerat - valid pentru argile compacte ( Nspt <30) medii și moi ( Nspt <4) și argile nisipoase (Nspt=6-12).
Modulul lui Young [Ey (Kg/cmp)]
•Schultze-Menzenbach (Min. și Max.), corelație valabilă pentru prafuri coezive și prafuri argiloase cu I.P > 15
•D'Appollonia și alții (1983) - corelație validă pentru argile saturate-argile fisurate.
Starea de consistență
•Clasificare A.G.I. (1977)
Greutate Volumică (t/mc)
•Meyerhof și alții - validă pentru argile, argile nisipoase și prăfoase prevalent coezive.
Greutate Volumică saturată
•Meyerhof și alții.
© GeoStru |