Tutte le aste previste nel programma presentano la stessa formulazione della matrice di rigidezza K nel sistema di riferimento locale x, y, z definito per le travi nel § 1.7.2. La matrice è simmetrica ed ha dimensioni 12x12:
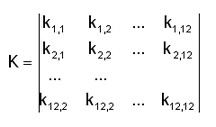
in cui tenendo conto di tutte le deformazioni (assiale, tagliante, torcente,flettente) i termini ki,,j non nulli con indice i ≤ j valgono:
k1,1 = E A / L
k1,7 = - E A / L
k2,2 = 12 E Jz / L³ Φy
k2,6 = 6 E Jz / L² Φy
k2,8 = -12 E Jz / L³ Φz
k2,12 = 6 E Jz / L² Φy
k3,3 = 12 E Jy / L³ Φz
k3,5 = -6 E Jy / L² Φz
k3,9 = -12 E Jy / L³ Φz
k3,11 = -6 E Jy / L² Φz
k4,4 = E Jp / (q L)
k4,10 = -E Jp / (q L)
k5,5 = 4 E Jy / L Φz λz2
k5,9 = 6 E Jy / L² Φz2
k5,11 = 2 E Jy / L Φz λz1
k6,6 = 4 E Jz / L Φy λy2
k6,8 = -6 E Jz / L² Φy
k6,12 = 2 E Jz / L Φy λy1
k7,7 = E A / L
k8,8 = 12 E Jz / L³ Φy
k8,12 = -6 E Jz / L² Φy
k9,9 = 12 E Jy / L³ Φz
k9,11 = 6 E Jy / L² Φz
k10,10 = E Jp / (q L)
k11,11 = 4 E Jy / L Φz λz2
k12,12 = 4 E Jz / L Φy λy2
con:
L luce del tratto deformabile dell'asta
A area sezione trasversale
E modulo elastico per tensioni normali
G modulo elastico tangenziale = 0.5 E /(1+ μ) indicando con μ il modulo di Poisson
Jy, Jz, Jp i momenti di inerzia rispetto agli assi pincipali d'inerzia ed il momento d'inerzia polare
q fattore di torsione della sezione
Φy = 1/ (2 βy +1)
βy = 6 E Jzχy / (G A L²)
Φy = 1 / (2 βy +1)
λy1 =1 - βy
λy2 = 1+ βy/2
Φz = 1/ (2 βz +1)
βz = 6 E Jyχz / (G A L²)
Φz = 1 / (2 βz +1)
λy1 =1 - βy
λz2 = 1+ βz/2
χy, χz fattori di taglio della sezione nelle direzioni degli assi y e z
Questi termini si riferiscono ad un'asta con vincoli di piena congruenza con i nodi. Ovviamente essi vengono modificati, caso per caso, in presenza di svincolamenti nodali (cerniere, pattini, ecc.).
Per la simmetria della matrice per i termini con indice i>j risulta kj,i = ki,j
Nella finestra dei dati generali (§ 2.2.2) è possibile assegnare la rigidezza torsionale come percentuale di quella nominale (il CEB Model Code 90 consiglia di assumere il 30% del modulo G per tener conto della fessurazione per torsione). In programma questa riduzione viene effettuata non sul modulo G bensì direttamente sulle rigidezze a torsione k10,10, k4,10 (per non alterare il valore di G in quelle a taglio).
In zona sismica è possibile (non obbligatorio) ridurre percentualmente anche le rigidezze flessionali (§ 7.2.6 NTC). In programma questa riduzione (se richiesta nei dati generali) viene operata direttamente sui momenti d'inerzia Jy, Jz .
Se in corrispondenza di un qualsiasi pilastro il valore del parametro q definito dalla (7.3.2) NTC supera il valore di 0.1 è necessario mettere in conto la nonlinearità geometrica (§ 7.3.1 NTC). Le NTC suggeriscono in tal caso di incrementare (per q ≤ 0.2) gli effetti dell'azione sismica di un fattore pari a 1/(1-q). Il metodo indicato dalle NTC (metodo P-D) è applicabile correttamente solo nel caso di orizzontamenti rigidi nel proprio piano. Nel programma si è, pertanto, utilizzato un procedimento più generale valido anche in presenza di piani deformabili e basato sulla costruzione della matrice di rigidezza geometrica W da sommare a quella meccanica K con riferimento alle sole aste soggette a significativi valori dello sforzo normale (pilastri, pareti e travi verticali). I termini non nulli della matrice geometrica W (avente le stesse dimensioni 12x12 della matrice K) sono (vedi [16]):
w2,2 = 36 / g
w2,6 = 3 L g
w2,8 = - 36 g
w2,12 = 3 L g
w3,3 = 36 g
w3,5 = - 3 L g
w3,9 = -36 g
w3,11 = - 3 L g
w5,5 = 4 L² g
w5,9 = 3 L g
w5,11 = - L² g
w6,6 = 4 L² g
w6,8 = -3 L g
w6,12 = - L² g
w8,8 = 36 g
w8,12 = - 3 L g
w9,9 = 36 g
w9,11 = 3 L g
w11,11 = 4 L² g
w12,12 = 4 L² g
in cui:
g = N / (30 L)
N = sforzo normale
L = luce asta
Il calcolo dovrebbe essere iterativo in quanto il valore dello sforzo normale N è incognito. Per linearizzare il procedimento, evitando le iterazioni, si considera lo sforzo normale N costante e pari a quello della prima combinazione di carico (combinazione fondamentale SLU). Questa approssimazione è in genere accettabile per gli edifici in ca in quanto gli sforzi normali dovuti ai carichi verticali (amplificati a mezzo dei fattori di combinazione non sismici) ben difficilmente risultano inferiori agli sforzi normali delle combinazioni sismiche.
Per poter riferire la matrice di rigidezza agli assi X,Y,Z del sistema generale è necessario costruire la matrice C(6,6) dei coseni direttori dell'asta. Indicate con X1,Y1,Z1 e X2,Y2,Z2 le coordinate degli estremi deformabili del'asta nel sistema generale e con Xp,Yp,Zp le coordinate generali di un punto nello spazio appartenente al piano definito dagli assi locali x,y purchè non situalto sull'asse x locale, i termini ci,,j della matrice C sono dati da:
c1,1 = Lx / L
c1,2 = Ly / L
c1,3 = Lz / L
c2,1 = Yx / YL
c2,2 = Yy / YL
c2,3 = Yz / YL
c3,1 = Zx / ZL
c3,2 = Zy / ZL
c3,3 = Zz / ZL
in cui:
Lx = X2-X1
Ly = X2-X1
Lz = X2-X1
L = (Lx² + Ly² + Lz²)0.5
Zx = Ly (Zp-Z1) - Lz (Yp-Y1)
Zy = Lz (Xp-X1) - Lx (Zp-Z1)
Zz = Lx (Yp-Y1) - Ly (Xp-X1)
ZL = (Zx² +Zy² +Zz²)
Yx = c3,2 c1,3 - c3,3 c1,2
Yy = c3,3 c1,1 - c3,1 c1,3
Yz = c3,1 c1,2 - c3,2 c1,1
Con la matrice C dei coseni direttori viene costruita la seguente matrice di trasferimento T(12,12):
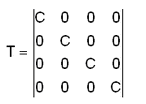
La matrice di rigidezza dell'asta K* dell'asta deformabile nel sistema di riferimento generale risulta:
K* = TT K T
in cui TT è la trasposta di T.
Per tener conto degli offset rigidi (conci rigidi) costituiti dalle eccentricità Ex1, Ey1,Ez1, Ex2, Ey2,Ez2 degli estremi deformabili dell'asta rispetto ai corrispondenti nodi è necessario trasferire la matrice K* ai centri dei nodi interessati. Viene pertanto costruita la seguente matrice di trasferimento U(12,12):
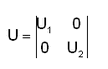
in cui le sottomatrici U1(6,6), U2(6,6) sono:
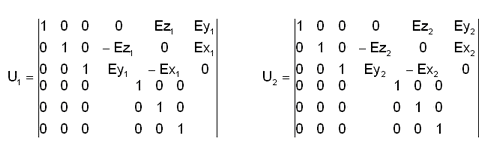
la nuova matrice K** diventa:
K** = UT K U
Nel caso in cui uno od entrambi i nodi dell'asta appartengano a diaframmi rigidi orizzontali (Z=cost.) cioè ai cosidetti piani rigidi (§ 1.2) è necessario un ulteriore trasferimento della matrice di rigidezza dell'asta in modo da riferirla ai nodi master dei rispettivi piani di appartenenza dei nodi. Allo scopo viene costruita questa ulteriore matrice di trasferimentoV(12,12):
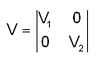
in cui le sottomatrici V1(6,6), V2(6,6) sono:
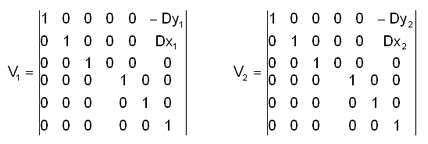
con:
Dx1 = XN1 - XG1 essendo XN1 l'ascissa del primo nodo dell'asta e XG1 l'ascissa del nodo master nel piano rigido a cui appartiene il nodo stesso
Dy1 = YN1 - YG1 essendo YN1 l'ordinata del primo nodo dell'asta e YG1 l'ordinata del nodo master nel piano rigido a cui appartiene il nodo stesso
Dx2 = XN2 - XG2
Dy2 = YN2 - YG2
In definitiva la matrice di rigidezza finale K*** dell'asta nel sistema generale è data da:
K*** = VT K V
L'assemblaggio delle matrici K*** di tutte le aste avviene sommando nella matrice A di rigidezza globale i singoli termini ki,j nel nella competente posizione am,n determinata dalla corrispondenza dei gradi di libertà (incidenze nodali).
Analoghe trasformazioni vengono effettuate per l'assemblaggio delle forze di incastro perfetto delle singole aste nel vettore B dei termini noti del sistema (cioè delle forze di incastro perfetto riferite al sistema generale) .
La matrice di rigidezza della singola trave di fondazione su suolo elastico alla Winkler viene invece costruita a partire da quelle dei singoli conci in cui la trave viene discretizzata (vedi § 1.7.5). Più precisamente le matrici di rigidezza dei conci di una stessa trave riferite ai rispettivi sistemi locali x,y,z, vengono assemblate in un'unica matrice K(12,12) insieme alle rigidezze delle molle elastiche che schematizzano il terreno. Alle estremità deformabili I e J della trave vengono applicate successive combinazioni di carico corrispondenti a singoli cedimenti e rotazioni unitari dei due nodi di estremità I e J. L'insieme ordinato dei vettori soluzione del sistema costituisce la matrice di deformabilità dell'intera asta I,J che, una volta invertita, rappresenta la cercata matrice di rigidezza K dell'asta I,J nel sistema locale. Questa matrice viene quindi assemblata nella matrice di rigidezza globale della struttura con lo stesso procedimento già esposta per le aste in elevazione.
Questa tecnica che permette di assimilare ogni trave di fondazione ad una sottostruttura consente di ridurre sensibilmente le dimensioni del sistema globale in quanto restano esclusi i gradi di libertà dei nodi generati dalla discretizzazione.
Nelle travi di fondazione su suolo elastico vengono assunti come vincolati i gradi di libertà nodali corrispondenti alle traslazioni nel piano X,Y e quello alla rotazione intorno all'asse Z; ciò comporta, per tutte le aste, rigidezza assiale e flettente nulla nel piano X,Y (ammesa solo flessione retta con taglio e torsione).
Geostru Software ©