Aspecte teoretice > Metoda CRSP

Metoda de calcul CRSP

Modelul numit CRSP (Colorado Rockfall Simulation Program) a fost pus la punct de Pfeiffer și Bowen (1989) cu scopul de modela căderea de blocuri cu formă sferică, discuri sau cilindri, cu secțiunea circulară pe planul vertical de mișcare.

Pentru a descrie mișcarea blocurilor modelul CRSP aplică ecuația de mișcare parabolică a unui corp în cădere liberă și principiul conservării energiei totale.

Fenomenul de impact este modelat utilizând ca și parametri ulteriori, cu referire la Metoda maselelor concentrate ( Lumped mass) , asprimea taluzului și dimensiunile blocurilor.

În particular modelul CRSP presupune că unghiul format între direcțiile blocului și taluzul în funcție de o statistică care trebuie definită pentru fiecare caz analizat. Modelul tratează statistic și rezultatele care în principal constau în vitezele și înălțimile de salt, în funcție de suprafața taluzului, în timpul căderii. Modelul consideră deci combinațiile de mișcări de cădere liberă, de salt, de rostogolire și de alunecare, care pot varia în funcție de dimensiunile blocurilor și de rugozitatea versantului.

Exactitatea modelului a fost verificată prin intermediul comparației dintre rezultatele numerice și cele obținute prin încercări în teren.

Descrierea mișcării de cădere liberă începe din punctul în care se cunoaște viteza inițială descompusă în cele două componente inițiale: orizontale și verticale. Blocul este supus mișcărilor de cădere liberă până în momentul în care se ciocnește cu versantul.

Din intersecție se află coordonatele punctului de impact. Vectorul vitezei de pre-impact V formează un unghi cu taluzul.

La fiecare impact înclinația taluzului variază între valori cuprinse între 0 și o valoare în funcție de asprimea taluzului și de dimensiunea blocului.

Viteza care se obține după impact este determintă cu ajutorul ecuației de conservare a energiei:

unde:

M = Masa blocului;

J = Momentul de inerție al blocului;

ω1 = Viteza unghiului înainte de impact;

ω2 = Viteza unghiului după impact;

Vt1 = Viteza tangențială înainte de impact;

Vt2 = Viteza tangențială după impact.

Funcția f(F) de forfecare definită după cum urmează:

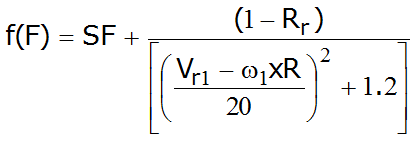
În schimb ce funcția de scară SF este:

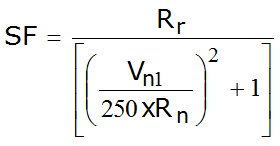
unde:

Rn = Coeficientul de restituire normalăi;

Rt = Coeficientul de restituire tangențială;

R = Raza blocului.

Termenii f(F) și SF sunt aflați prin intermediul expresiilor empirice care se utilizează pentru valutarea energiei cinetice disipată în coeziuni între bloc și taluz din cauza forfecării și al ciocnirii.

Forfecarea privește în principal disiparea energiei produsă de viteza tangențială, ciocnirea produsă de către viteza normală a taluzului.

Vitezele tangențiale și unghiulare post-coeziune sunt puse în relație între ele de următoarea experesie:

Vt2 =ω2 × R

care presupune că blocurile abandonează contactul cu taluzul rotindu-se, independent de viteza unghiulară precedentă.

Din (1) se obține Vt2, în timp ce viteza normală post-coeziune este calculată cu următoarea expresie empirică:

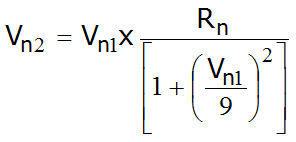
care vrea să țină cont de faptul, verificat și experimental , că raportul între vitezele normale post-impact și pre-impact se micșorează cu creșterea a însăși vitezei normale pre-impact.

Lista simbolurilor

x(), y() = Coordonatele punctelor taluzului în m;

Rn, Rt = Coeficientul de restituire normală și tangențială;

rugosità = Asprimea taluzului;

Xp, Yp = Coordonatele punctului de plecare al stâncii;

xi, yi = Coordonatele punctului de impact;

vx, vy = Viteza de pre-impact a blocului;

t = Durata zborului în secunde;

E() = Energia de pre-impact în Joule.