CRSP method
The CRSP model (Colorado Rockfall Simulation Program) has been developed by Pfeiffer and Bowen (1989) with the purpose of modeling the falling motion of boulders having the shape of spheres, cylinders or discs, with circular cross section in the vertical plane of the movement.
To describe the movement of the boulders the CRSP model applies the parabolic equation of motion of a body in free fall and the principle of conservation of the total energy.
The phenomenon of the impact is modeled using as additional parameters, compared to the Lumped Mass method, the roughness of the slope and the size of boulders.
In particular, the CRSP model assumes that the angle formed between the direction of the boulder and the profile of the slope varies according to a statistic that must be defined for each analyzed case. The model considers statistically also the results that mainly consist in the velocities and bounce heights, as compared to the surface of the slope, during the fall path. So the model considers the combinations of movements of free fall, of bounce, rolling and slipping, which can vary depending on the size of the boulders and the roughness of the slope.
The reliability of the model was verified by comparisons between numerical results and the results obtained from in situ tests.
The description of the motion of free fall starts from a point in which the initial velocity is known and is decomposed into its horizontal and vertical components. The boulder is subjected to the movement of free fall until it collides with the surface of the slope.
From the intersection are obtained the coordinates of the impact point. The velocity vector of pre-impact V, forms an angle α with the slope.
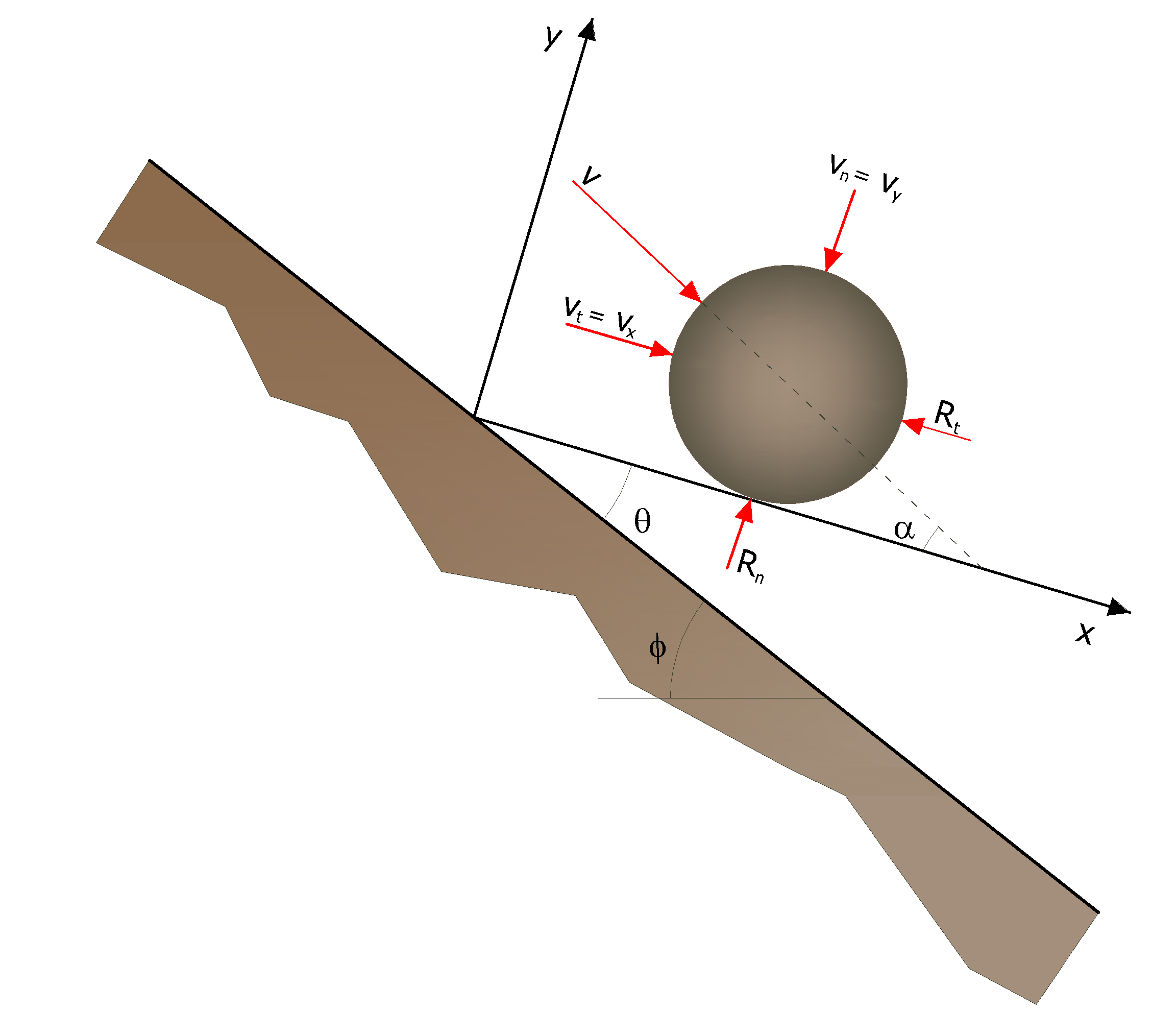
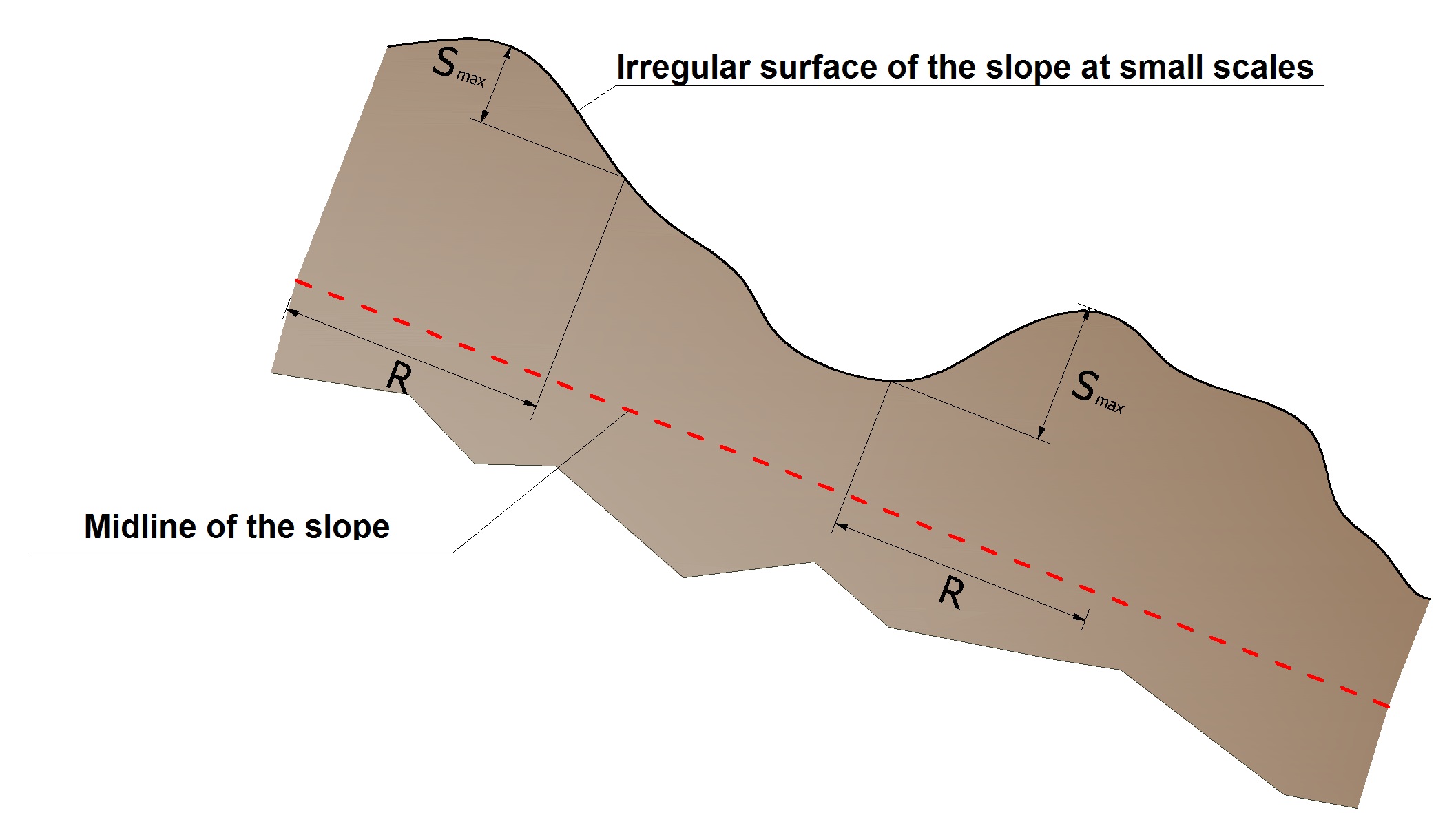
For each impact, the angle of the slope ϕ is varied randomly in a range of values between 0 and θmax. The value of θmax depends on the roughness of the slope and on the size of the boulder and is determined by in situ measurements. Being R the radius of the boulder under consideration we have:
![]()
The angle θmax is defined as the maximum variation of the average inclination compared to the radius R of the boulder.
The velocity that is obtained as a result of the impact is determined by the conservation equation of the total energy expressed as follows:
![]()
where:
R |
Radius of the boulder |
M |
Mass of the boulder |
J |
Moment of inertia of the boulder |
ω1 |
Angular velocity before impact |
ω2 |
Angular velocity after impact |
Vt1 |
Tangential velocity before impact |
Vt2 |
Tangential velocity after impact |
The function of friction f(F) is defined:

While the scale function SF is defined:
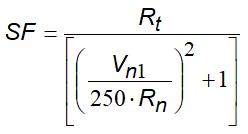
The terms f(F) and SF are obtainable through empirical expressions that are used to assess the kinetic energy dissipated in collisions between the boulder and the slope because of friction and impact.
The friction is primarily concerned with the dissipation of the energy produced by the tangential velocity, while the impact the energy produced by the velocity normal to the slope.
The tangential and angular post-collision velocities are related between them by the following equation:
![]()
which assumes that the boulders leave the contact with the slope rotating, regardless of the previous angular velocity.
The normal post-collision velocity is obtained by the following empirical expression:
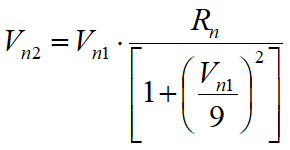
that will to take account of the fact, also verified experimentally, that the ratio between the normal post-impact and pre-impact velocities decreases with the increase of the normal pre-impact velocity itself.
Rn |
Normal restitution coefficients |
Rt |
Tangential restitution coefficients |
R |
Radius of the boulder
|
|
© GeoStru