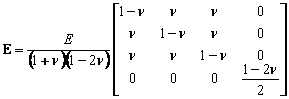Axisymmetric elementsare defined as having a constant value of displacement in the circumferential or θ direction. These are similar to the two-dimensional element, except that it is used in the r-z plane as shown in Fig. 17.
The stress and strain components for the element are:
|
|
(29) |
where the strains are defined as follows, with u and w being the displacements in the r and z directions respectively:
|
|
(30) |
|
Fig. 17. Basic axisymmetric element and stress components. |
The constitutive matrix that linking the stresses and strains is:
|
|
(31) |
where E is the Young's modulus, ν the Poisson's ratio.
The two-dimensional isoparametric finite elements employed in GFAS are linear and quadratic triangles and quadrilaterals. Isoparametric finite elements are based on the parametric definition of both coordinate and displacement functions. The same shape functions are used for specification of the element shape and for interpolation of the displacement field.
|
© GeoStru Software