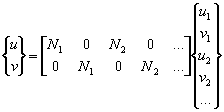<< Click to Display Table of Contents >> Navigation:  Formulation of the element matrices and vectors for elasticity problem > Finite element types

 

Displacements (u, v) in a plane element are interpolated from nodal displacements (ui, vi) using shape functions Ni as follows:

 

                                       

                                                                         

where N is the shape function matrix, u the displacement vector and d the nodal displacement vector. Here we have assumed that u depends on the nodal values of u only, and v on nodal values of v only.

 

From strain-displacement relation, the strain vector is:

 

                                                             

where

 

                                                             

is the strain-displacement matrix.

 

Consider the strain energy stored in an element:

 

 

     

From this, we obtain the general formula for the element stiffness matrix:

 

                                                             

where the constitutive matrix E is given by the stress-strain relation. The stiffness matrix k defined by the above formula is symmetric since the constitutive matrix E is symmetric.

 

 

 

 

 

 

 

 

© GeoStru Software