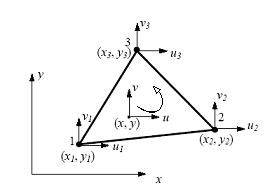
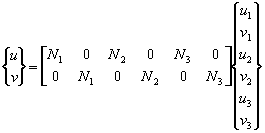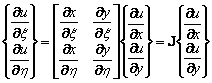Formulation of the element matrices and vectors for elasticity problem > Finite element types

The two-dimensional simplex element is a triangle as shown in Fig. 18, it has two degrees of freedom at each node. It is also called linear triangular element.

p_25_image010

Fig. 18. Linear triangle finite element (T3)

For this element, we have three nodes at the vertices of the triangle, which are numbered around the element in the counterclockwise direction. Each node has two degrees of freedom (can move in the x and y directions). The displacements u and v are assumed to be linear functions within the element that is:

(38)

The constants α and β are determined imposing the nodal conditions. Solving the system of equations we can find the coefficients in terms of nodal displacements and coordinates.

p_26_image002

Fig. 19 The natural coordinates for linear triangle finite element

Introducing the natural coordinates (ξ, η) on the triangle (Fig.19), the shape functions can be represented by:

(39)

Thus, in terms of nodal d.o.f the displacement field is:

p_26_image006

(40)

We have two coordinate systems for the element: the global coordinates (x, y) and the natural coordinates (ξ, η). The relation between two is given by:

(41)

Displacement u or v on the element can be viewed as functions of (x, y) or (ξ, η). Using the chain rule for derivatives, we have:

p_26_image010

(42)

where J is called the Jacobian matrix of the transformation.