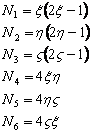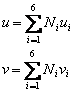<< Click to Display Table of Contents >> Navigation:  Formulation of the element matrices and vectors for elasticity problem > Finite element types > Linear Strain Triangle (T6)

 

This element is also called quadratic triangular element.

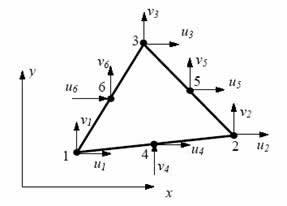
There are six nodes on this element: three corner nodes and three mid-side nodes (Fig.20). Each node has two degrees of  freedom (DOF). The displacements (u, v) are assumed to be quadratic functions of (x , y).

 

 

 

 

 

                                 

From these, the strains are linear functions, thus we have the "linear strain triangle" (LST), which provides better results than the CST.

 

In the natural coordinate system, defined earlier, the six shape functions for the LST element are:

 

 

                                                             

in which .

 

Displacements can be written as:

 

                                                     

The element stiffness matrix is still given by:

 

                                                           

but here BTEB is quadratic in x and y. The integral is computed numerically.

 

 

 

 

 

 

 

 

© GeoStru Software