La Figura 15 mostra un elemento infinitesimo piano su cui si mettono in evidenza le componenti vettoriali di tensione sui suoi lati inoltre sono presenti pure le quantità fx e fy componenti della forza di volume “forza gravitazionale”.
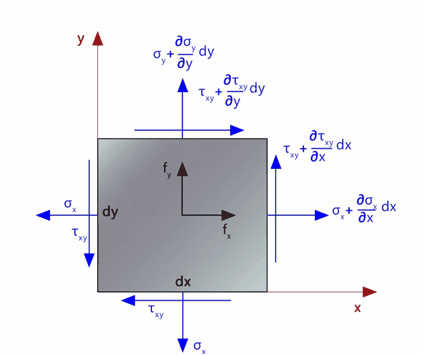
Fig. 15. Tensioni e forze di volume che agiscono su un elemento
differenziale piano di spessore costante.
L’equilibrio alla traslazione fornisce le due equazioni indefinite di equilibrio che definiscono un legame differenziale tra le componenti del tensore degli sforzi e le forze di volume mentre l’equilibrio alla rotazione conferma la simmetria del tensore di Cauchy :
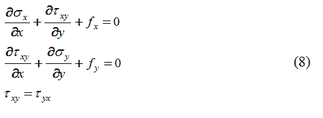
Nel metodo degli elementi finiti le suddette equazioni differenziali di equilibrio risultano soddisfatte in senso approssimato in qualsiasi punto del mezzo.