Riferendoci alla Figura 44, se in un punto A, che giace all’interno o sulla superficie di rottura, è applicato un predittore elastico, questo produce uno stato tensionale al di fuori della superficie e, pertanto, gli incrementi terminano nel punto B. Per soddisfare la condizione di rottura è applicato un correttore plastico, che restituisce le tensioni sulla superficie di rottura, in particolare nel punto C. Il correttore plastico è determinato da due quantità, il valore scalare ∆λ, che rappresenta il valore della magnitudine, e il gradiente di carico 
che fornisce la direzione. Lo scalare ∆λ è determinato se la condizione di rottura è soddisfatta:
dove ∆σp è dato da:
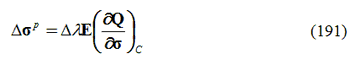
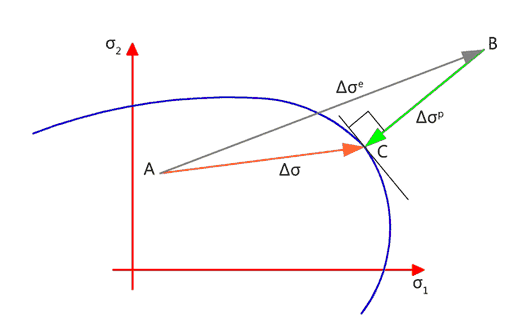
Fig. 44. Correzione della tensione.
Se si espande in serie di Taylor la funzione di snervamento valutata nel punto B, l’elemento di primo ordine assume la seguente forma:
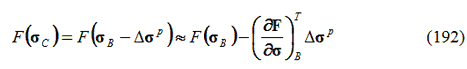
Se si inserisce l’espressione fornita per ∆σp nell’espressione sopra riportata e ricordando che la funzione di snervamento è costante nel punto C, si ottiene un passo:
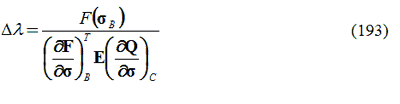
con lo schema di integrazione all’indietro di Eulero, è possibile formare una matrice modulare tangente costante:
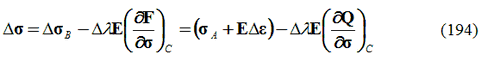
differenziando si ottiene:
dove Ecep è nota come “matrice tangente costante” ed è data da:
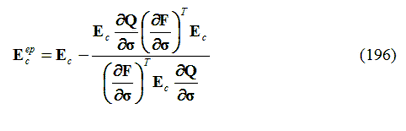
e inoltre:
