Siano F i carichi applicati sulla struttura con incrementi ∆F1 ∆F2 e così via, in modo tale che 
. L’interpretazione grafica del metodo per un problema con una sola variabile spostamento è mostrata nella Figura 45, dove i pedici i indicano il numero di step effettuati.
La procedura si può sintetizzare nei seguenti passi:
1.Per il primo ciclo di calcolo (i=1) si assume Eep=E per tutti gli elementi. Si applica, dunque, il primo incremento di carico ∆F.
2.Utilizzando le deformazioni correnti, si determina il valore di Eep in ciascun elemento, ottenendo il valore di kt per ognuno di essi. Quindi, si determinano i valori delle forze residue, si ottiene la matrice Kt,i globale di rigidezza tangente e si risolve il sistema
. Tramite il valore di ∆Ui si ottiene l’incremento corrente della deformazione ∆εi per ciascun elemento.
3.Se qualche elemento effettua il passaggio dallo stato elastico a quello plastico si corregge il valore di Eep e si ritorna allo step 2 ripetendo gli step 2 e 3 fino alla convergenza.
4.Si aggiorna il vettore spostamento 
, le deformazioni 
e le tensioni 
.
5.Si applica l’incremento di carico successivo e si ritorna allo step 2.
6.La procedura si arresta quando la somma degli incrementi di carico uguaglia il carico totale oppure quando la struttura collassa.
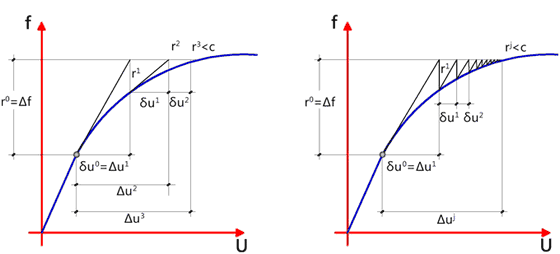
(a) Procedura completa di Newton-Raphson
(b) Procedura modificata di Newton-Raphson.
Fig. 45. Procedura di risoluzione
Solitamente si utilizza il cosiddetto metodo di Newton-Raphson modificato.
La modifica consiste nel valutare la rigidezza tangente solamente una volta all’inizio di ogni step di carico anziché in ogni iterazione, come mostra la Figura 45 (b). Pertanto, durante lo step 2 dell’algoritmo mostrato in precedenza, la matrice delle rigidezze tangente è assemblata e fattorizzata solamente una volta e cioè all’inizio degli incrementi di carico. Durante il processo d’iterazione si valutano le forze residue.
Si dice che la convergenza sia verificata se il valore assoluto della variazione di tutte le componenti del vettore delle forze residue tra il valore corrente ed il valore massimo risulta minore di un predefinito valore di tolleranza.