In questo metodo il materiale è capace di sostenere tensioni al di fuori del criterio di rottura per un “periodo finito”, per cui anziché alle deformazioni plastiche, ci si riferisce alle deformazioni visco-plastiche, il cui valore è legato alla quantità con cui il criterio di resistenza viene violato. Le deformazioni visco-plastiche sono date da:

dove F è la funzione di snervamento e Q è la funzione potenziale plastico.
L’incremento della deformazione visco-plastica, che si accumula iterazione dopo iterazione, si ottiene moltiplicando il tasso di deformazione per un passo temporale fittizio come mostrano le Equazioni 165 e 166:

e

in cui il passo temporale, per la stabilità numerica, dipende dal criterio di rottura, che si assume come mostrato di seguito:
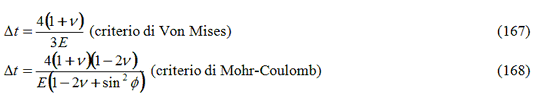
Le derivate della funzione potenziale plastico Q, rispetto alle tensioni, si può esprimere come:
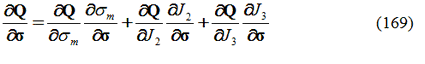
dove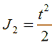 .
.
Il parametro t rappresenta il secondo invariate deviatorico delle tensioni (Equazione 170):
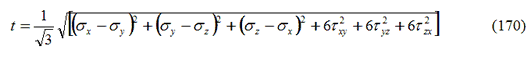
e
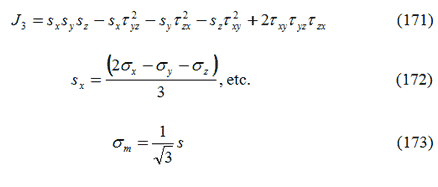
Il primo invariante s è dato dalla relazione:
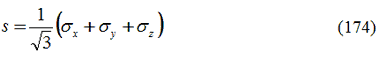
Questo si può notare sopratutto nelle applicazioni di tipo geotecnico: si applicano le condizioni di deformazione piana e nelle equazioni di cui sopra si sostituisce la condizione ![]() .
.
La componente della deformazione visco-plastica si può calcolare numericamente con l’Equazione 175:
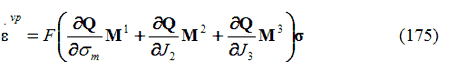
dove
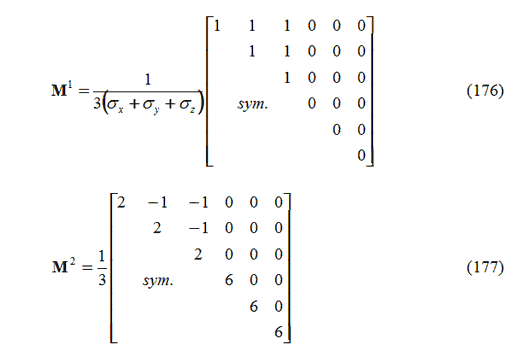
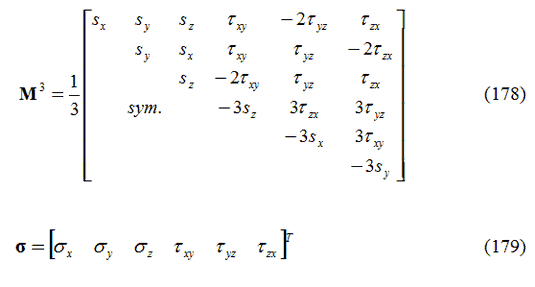
I carichi di volume auto-equilibrati si accumulano, in ogni passo temporale e per ogni step di carico, sommando i seguenti integrali valutati in tutti i punti di Gauss che non soddisfano il criterio di rottura (F>0 ai punti di Gauss).
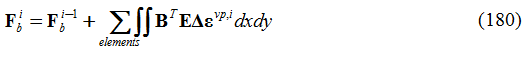
Questo processo si ripete per ogni passo temporale finché nessun punto di integrazione sollecitato viola il criterio di rottura rispettando una data tolleranza.
La convergenza del criterio è basato su una misura adimensionale con cui varia il valore del vettore incremento dello spostamento Ui iterazione dopo iterazione.