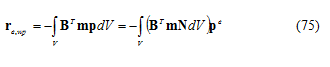L’effetto della superficie libera sul suolo compatto può essere preso in considerazione in due modi: il primo consiste nella valutazione dello spettro idrostatico valutando la pressione dell’acqua nei pori del terreno sia attraverso un’analisi rigorosa dello stato stazionario e sia attraverso un carico esterno causato dalla falda che agisce sulla massa.
La pressione interstiziale è calcolata in tutti i punti sommersi (integrazione di Gauss) e sottratta dalle tensioni normali totali calcolata nelle stesse posizioni considerando la superficie libera e i carichi gravitazionali. Le tensioni effettive risultanti sono così utilizzate nella restante parte dell’algoritmo relativa alla valutazione della funzione di snervamento e alla ridistribuzione delle tensioni elasto-plastiche.
Se chiamiamo con p la pressione neutra interstiziale, definita come un potenziale delle forze di volume, su un elemento infinitesimo agiranno, in direzione x-y del piano, le seguenti forze:
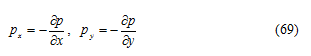
Si considera un elemento finito con nodi i, j, k se il potenziale delle forze di volume ai nodi è pari a pi pj pk allora il potenziale delle forze per l’elemento considerato può essere scritto come:
![]()
Poiché per il potenziale si possono scegliere le stesse funzioni di forma utilizzate per il campo degli spostamenti dell’elemento finito, si può scrivere in modo analogo:
![]()
L’effetto della pressione neutra interstiziale produce delle tensioni normali σ’0, che per l’analisi di deformazione piana è data da:
![]()
E per il caso di deformazione piana:

Il vettore delle tensioni totali quindi assume la seguente forma:
![]()
Di conseguenza, le equazioni generali di equilibrio, date dall’Equazione 21, possono essere generalizzate introducendo il seguente termine nel vettore degli elementi dei carichi nodali equivalenti tenendo conto in questo caso dell’effetto delle pressioni interstiziali: