Il vettore dei carichi nodali costanti re dato dall’Equazione (21) converte i carichi distribuiti su un elemento o sulla sua superficie o causati da una deformazione o sollecitazione iniziale, in carichi discreti sui nodi. Questi sono definiti costanti perché sono basati sulle stesse funzioni di forma come quelle utilizzate per calcolare gli elementi che compongono la matrice delle rigidezze. Peraltro questi carichi sono staticamente equivalenti ai carichi distribuiti originari: sia re e sia i carichi originari hanno la stessa risultante delle forze e lo stesso momento risultante calcolato rispetto a qualsiasi punto scelto in modo arbitrario.
Questi carichi sono chiamati carichi di esercizio equivalenti per la seguente ragione: il lavoro svolto dai carichi nodali re per ottenere lo spostamento nodale d è uguale al lavoro compiuto dai carichi distribuiti F e Ф per ottenere il campo di spostamento associato alla funzione di forma dell’elemento:
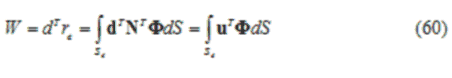
L’ultimo integrale somma il lavoro compiuto dall’incremento delle forze ФdS per ottenere u, dove u è campo degli spostamenti creato da d attraverso le funzioni di forma.