Dopo aver valutato le matrici e i vettori di ogni elemento, segue il processo di assemblaggio per computare il sistema globale delle equazioni. La soluzione del sistema globale di equazioni fornisce gli spostamenti nei nodi del modello ad elementi finiti. Ottenuti i risultati si calcolano le deformazioni e le tensioni in ciascun elemento. Per problemi in campo elastico, le deformazioni in un elemento sono calcolate a partire dagli spostamenti come:
![]()
Negli elementi semplici, come ad esempio nel CST, la matrice B Deformazione-Spostamento è costante, pertanto le deformazioni sono costanti e si possono calcolare dovunque nell’elemento.
Per gli elementi ad 8 nodi, invece, B è funzione del sistema di coordinate (spostamenti) e non sempre è una funzione esplicita. Pertanto le deformazioni devono essere valutate in posizioni specifiche in ciascun elemento. La localizzazione che fornisce risultati più accurati è quella utilizzata per i dei punti di campionamento con cui si sono determinate la matrice Deformazione-Spostamento B e la matrice delle rigidezze k. Le tensioni sono calcolate con le leggi di Hooke. Queste tensioni possono essere stimate ovunque nell’elemento ma hanno una migliore precisione se valutate nei punti di integrazione di Gauss.
Per esempio per l’elemento quadrangolare a 4 nodi le sollecitazioni hanno una maggiore precisione se valutate nei punti di integrazione 2x2 come mostra la Figura 23.
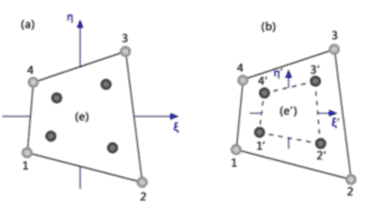
(a) Regola 2x2. (b) Elemento di Gauss (e’)
Fig.23. Estrapolazione dei punti di campionamento di un
elemento quadrangolare a 4 nodi
Al fine di costruire un campo continuo delle tensioni è necessario estrapolare i valori risultati dai punti di integrazione ai nodi degli elementi finiti. Le tensioni ai nodi, particolarmente nei vertici dell’elemento, sono molto importanti. Per calcolare le tensioni nodali, anche la matrice B deve essere valutata nei nodi, oppure le tensioni devono essere interpolate a partire dai valori ottenuti dai punti di campionamento. Un possibile modo per creare un campo continuo delle tensioni con una buona accuratezza consiste nel:
1) estrapolare le tensioni per ridurre i punti di integrazione ai nodi;
2) valutare i contributi medi per gli elementi finiti a tutti i nodi del modello.
Il processo di interpolazione-estrapolazione è descritto come segue.
Si assume che le tensioni possono essere valutate ai quattro punti di Gauss di un elemento quadrangolare piano. Si vogliono interpolare o estrapolare le tensioni degli altri punti dell’elemento. Nella Figura 23, la coordinata ξ’ è proporzionale a ξ e η’ è proporzionale a η. Nel punto 3’, ξ’=1 , η’=1 e ξ= η=1/![]() . Cioè:
. Cioè:

Le tensioni in ogni punto P dell’elemento sono date dalle funzioni di forma assunte per l’interpolazione del campo di spostamento:

dove σ include le componenti σx , σy , τxy.
Le funzioni di forma Ni sono funzioni bilineari:

Le funzioni di forma si valutano nelle coordinate ξ’ e τ’ del punto P. Per esempio, lasciando coincidere il punto P con un vertice, per calcolare la tensione σx nel nodo a partire dal valore σx valutato ai quattro punti di Gauss, si sostituisce la relazione ξ’= η’=1/![]() nelle funzioni di forma definite sopra e si applica la formula data nell’Equazione (53).
nelle funzioni di forma definite sopra e si applica la formula data nell’Equazione (53).
Nel caso degli elementi triangolari si applica un approccio del tutto simile. Per esempio per gli elementi triangolari di ordine superiore, a 6 nodi, e con 3 punti di Gauss, le tensioni in ogni punto dell’elemento sono computate usando le funzioni di forma come:

Dove le funzioni di forma sono definite da:

Valutate nelle coordinate ξ’ e τ’:

Come già detto, queste quadrature sono di ordine inferiore per elementi di ordine superiore, e rappresentano quello che viene definito schema di integrazione ridotta. Lo schema di integrazione ridotta è preferibile per due ragioni.
Innanzi tutto l’onere computazionale necessario a generare una matrice di elementi finiti per l’integrazione numerica è proporzionale al numero dei punti di campionamento, cosicché utilizzando meno punti di campionamento si ha un onere minore.
Secondo, leggi di ordine inferiore tendono a contrarre un elemento in modo da opporsi al comportamento eccessivamente rigido associato al campo di spostamento ipotizzato. Le tensioni sono generalmente mediate ai nodi nei Software che effettuano le Analisi agli Elementi Finiti (FEA) per ottenere una maggiore accuratezza nei valori.
Questa opzione può essere disattivata ai nodi compresi fra due materiali differenti o in corrispondenza di discontinuità esistenti. Le tensioni e le deformazioni al centro dell’elemento si ottengono attraverso l’estrapolazione delle tensioni dai punti di integrazione di Gauss.
Il programma è implementato da una tecnica molto efficiente chiamata Super Convergence Patch Recovery (SCP). Fondamentalmente il metodo utilizza il concetto della correzione locale di una porzione dell’elemento campionata nei punti di integrazione per produrre una serie regolare dei minimi quadrati adatta a rappresentare le tensioni nodali (Figura 24).
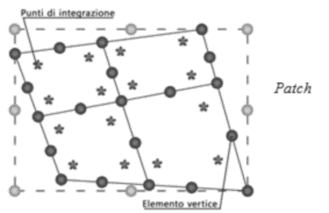
Fig. 24. Super Convergent Patch Stress Recovery.
Come appena detto, i punti di integrazione sono dei punti speciali dove le tensioni assumono i valori più attendibili. L’utente è spesso interessato non solo alle singole componenti delle tensioni, ma anche al valore della tensione globale come la tensione di Von Mises.
Nel caso di tensione piana, le tensioni di Von Mises sono date da:
![]()
Dove σ1 e σ2 sono le tensioni principali date da:
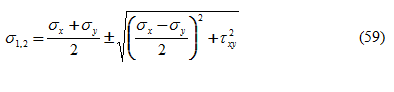
L’angolo formato dalle direzioni delle tensioni principali (Figura 25) si determina come:
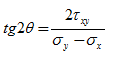
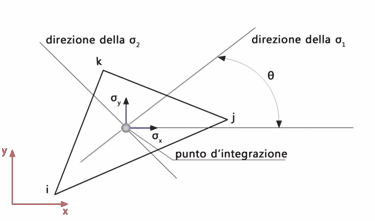
Fig. 25. Tensioni principali
Il post-processor mostra il contorno della sollecitazione che è tipicamente prodotto lavorando sulle tensioni nodali medie. Questi contorni possono essere visualizzati come ‘stress bands’ designando degli intervalli equispaziati di sollecitazione, localizzando le aree di ciascun elemento che ricade in ogni intervallo, e utilizzando diversi colori per rappresentare ognuno di esso.