L’integrazione delle equazioni che definiscono le matrici di rigidezza e i vettori di carico non può essere eseguita analiticamente per il caso generale degli elementi isoparametrici. Invece, le matrici di rigidezza e i vettori di carico sono valutati numericamente utilizzando la regola della quadratura di Gauss, applicabile a regioni di forma triangolare e quadrangolare.
La formula della quadratura di Gauss per il dominio di integrazione nel caso bidimensionale espressa in coordinate naturali è:
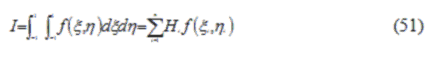
In cui i valori di Hi sono le funzioni di peso necessarie all’applicazione della regola integrazione di Gauss, mentre (xi,hi) sono le coordinate di opportuni punti nell’intervallo (in gergo punti di Gauss o punti di campionamento). I punti di campionamento e le funzioni di peso sono utilizzate nel caso di elementi quadrangolari come mostrato nella Tabella 3. Si utilizza uno schema 2x2 o 3x3, in base all’ordine della funzione che deve essere valutata.
Generalmente la formulazione a 4 punti è utilizzata per gli elementi quadrangolari a 4 nodi, mentre quella a 9 punti per gli elementi ad 8. La matrice delle rigidezze dell’elemento quadrangolare generale ad 8 nodi contiene termini polinomiali del quarto ordine e così richiede 9 punti di campionamento per effettuare l’integrazione. Accade spesso che l’uso dell’integrazione di riduzione utilizzando i 4 punti migliora le prestazioni dell’elemento. Questo è particolarmente vero nelle applicazioni di tipo plastico. I pesi e i punti della quadratura per gli elementi triangolari (T3 e T6) sono riassunti nella Tabella 4.
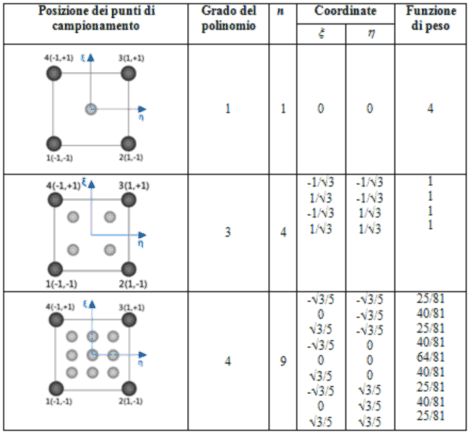
Tabella 3. Pesi e punti di campionamento della quadratura di Gauss per elementi quadrangolari.
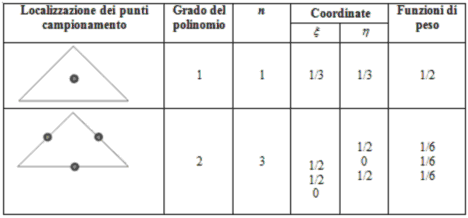
Tabella 4. Pesi e punti di campionamento della quadratura di Gauss per elementi triangolari.