Per cedimento si intende l’abbassamento del piano campagna, ovvero l’integrale della deformazione del terreno in direzione verticale, o anche la sommatoria dei prodotti della deformazione verticale media per lo spessore di ciascuno degli strati deformati.
Il cedimento permanente indotto dall’azione sismica in corrispondenza di una verticale di esplorazione si ottiene dalla somma dei contributi al cedimento stimati per i diversi strati del sottosuolo, fino alla profondità alla quale tali
contributi non sono più significativi. Il cedimento permanente post-sismico può dunque essere stimato con l’equazione:
![]()
in cui εvi è la deformazione volumetrica (e verticale) dello strato i-esimo e Δzi il suo spessore.
I cedimenti permanenti indotti dall’azione sismica possono essere dovuti alle deformazioni volumetriche (e quindi verticali) di:
B1. terreni granulari saturi,
B2. terreni granulari insaturi,
B3. terreni coesivi soffici.
I cedimenti conseguenti a liquefazione di terreni granulari saturi hanno luogo immediatamente dopo il terremoto o comunque in un tempo non superiore a un giorno, i cedimenti per densificazione di terreni granulari insaturi avvengono durante lo scuotimento sismico, mentre i cedimenti per consolidazione di terreni coesivi molli possono richiedere tempi anche molto lunghi in funzione delle condizioni stratigrafiche e geotecniche.
Stima dei cedimenti indotti dall’azione sismica nei terreni granulari saturi
La deformazione volumetrica (e verticale) εv nei terreni granulari saturi può essere stimata da prove CPT in funzione della resistenza penetrometrica di punta normalizzata e corretta, (qc1N)cs e del coefficiente di sicurezza alla liquefazione FL con il grafico di Figura 3a (Zhang et al.,2002), e da prove SPT in funzione della resistenza SPT normalizzata e corretta (N1)60,cs e del rapporto di tensione ciclica CSR con il grafico di Figura 3b (Wu e Seed, 2004).
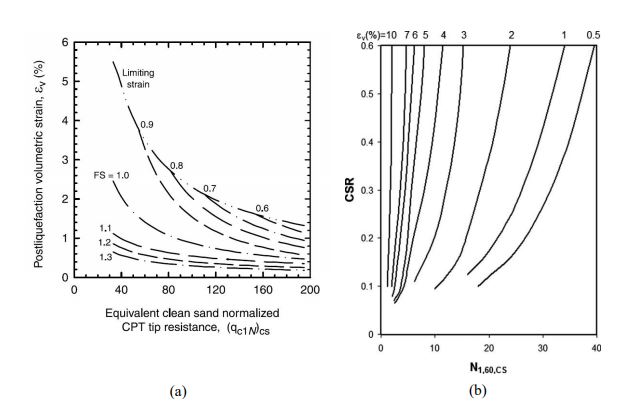
Carte per la stima delle deformazioni volumetriche indotte dall’azione sismica nei terreni granulari saturi sulla base dei risultati di prove CPT (a) (Zhang et al., 2002), e SPT (b) (Wu e Seed, 2004)
Stima dei cedimenti indotti dall’azione sismica nei terreni granulari insaturi
Il cedimento indotto dall’azione sismica nei terreni granulari insaturi può essere stimato dai risultati di prove SPT con il metodo di Pradel (1998), nel modo seguente:
![]()
in cui Δs è il cedimento dello strato di spessore Δz.
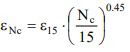
E' la deformazione volumetrica per un numero di cicli equivalente Nc il cui valore è funzione della magnitudo del terremoto secondo l’equazione: Nc=(M-4)2.17
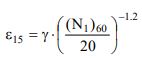
E' la deformazione volumetrica dopo 15 cicli di ampiezza γ , (N1)60 è il numero di colpi della prova SPT normalizzato alla pressione atmosferica, e γ è la deformazione di taglio media indotta dall’azione sismica.
Quest’ultima può essere determinata, in prima approssimazione, con la relazione empirica:
![]()
G è il modulo di taglio corrispondente al livello deformativo γ, che può essere determinato per via iterativa, noto il valore della rigidezza iniziale G0 (= ρVS2), utilizzando la legge di
variazione G(γ)/G0 ottenuta con prove dinamiche in laboratorio o, in modo approssimato, desunta da curve di letteratura per terreni con proprietà simili (si veda ad es. Figura 4 da AGI,
2005).
In alternativa la deformazione di taglio media indotta dall’azione sismica può essere stimata con la relazione empirica (Pradel, 1998):
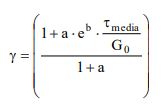
in cui
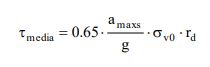
G0 è il modulo di taglio iniziale, che può essere determinato con la relazione G0 (= ρVS2) oppure stimato in prima approssimazione con relazioni empiriche in funzione dei risultati di prove in
sito (ad es. SPT, CPT, etc).
![]()
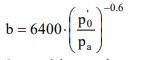
Ove pa è la pressione atmosferica e p’0 è la pressione media efficace alla profondità considerata
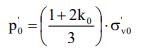
In mancanza di determinazione sperimentale si può assumere per il coefficiente di spinta a riposo k0 il valore 0.5.
Stima dei cedimenti indotti dall’azione sismica nei terreni coesivi soffici
Nei depositi coesivi soffici (cu ≤ 70kPa; VS < 180m/s) e plastici (IP ≥ 30%), in cui si prevede un incremento delle pressioni interstiziali Δu/p'0≥ 0.3 durante l’azione sismica di riferimento, la deformazione volumetrica (e verticale) e quindi l’entità del cedimento di riconsolidazione conseguente alla dissipazione delle pressioni interstiziali accumulatesi durante il terremoto può essere stimata con l’equazione (Yasuhara e Andersen, 1991):
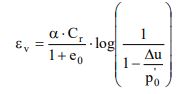
In cui:
Cr è l’indice di ricompressione, che si assume pari all’indice di rigonfiamento Cs, determinabile con prova edometrica oppure dalla relazione Cr=0.225·Cc
Il valore dell'indice di compressione Cc può essere stimato con le due seguenti formule:
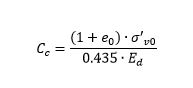
(Relazione di lambe e Witman 1969)
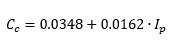
α=1.5 è un coefficiente empirico che tiene conto della particolare storia di carico ciclico,
e0 è l'indice dei vuoti naturali in situ dell'argilla
Δu/p'0= ru è il rapporto fra l’incremento di pressione interstiziale indotta dallo scuotimentosismico e la tensione media efficace iniziale.
Per la stima del rapporto di sovrapressione interstiziale può essere utilizzata la seguente relazione empirica (Matsui et al., 1980):
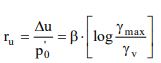
In cui
β=0.45 è un coefficiente sperimentale
γmax è la deformazione di taglio massima in semplice ampiezza indotta dal terremoto, determinabile, in prima approssimazione, con la relazione empirica:
![]()
G è il modulo di taglio corrispondente al livello deformativo γ, che può essere determinato per via iterativa, noto il valore della rigidezza iniziale G0 (= ρVS2), utilizzando la legge di
variazione G(γ)/G0 ottenuta con prove dinamiche in laboratorio o, in modo approssimato, desunta da curve di letteratura per terreni con proprietà simili (si veda ad es. Figura 4 da AGI,
2005).
γv è la deformazione di soglia volumetrica, determinabile con prove dinamiche di laboratorio, o in prima approssimazione con la relazione empirica (Matsui et al. 1980):
γv= A (OCR-1)+B
in cui OCR è il rapporto di sovraconsolidazione e A e B sono coefficienti sperimentali che, in assenza di determinazione diretta, possono essere stimati in funzione dell’indice di plasticità, IP (Tabella 1).
Tabella 1 - Valori suggeriti per i coefficienti A e B
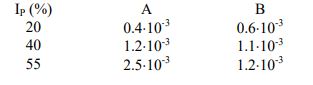
©Geostru