There are situations where it is impossible to maintain the resultant of the soil pressure within the middle third of the foundation base. This situation occurs when one or more combinations of load exceeds substantially the ability of the foundation to resist overturning moment (temporary or transient load conditions due to wind or earthquake). Although the foundations are usually not designed for such loading conditions, their stability to overturning should be tested in the presence of these temporary loads.
The geotechnical consultant should provide, on request, a separate assessment of the allowable pressure on the soil q'0 valid for temporary load conditions, in addition to the one used for the operating conditions.
For an eccentricity
![]()
regarding one axis, we obtain an equation from the following figure to determine the maximum pressure on the soil and the effective length L' of the foundation, where it is obvious that the base area is not reacting for a length equal to L - L'.
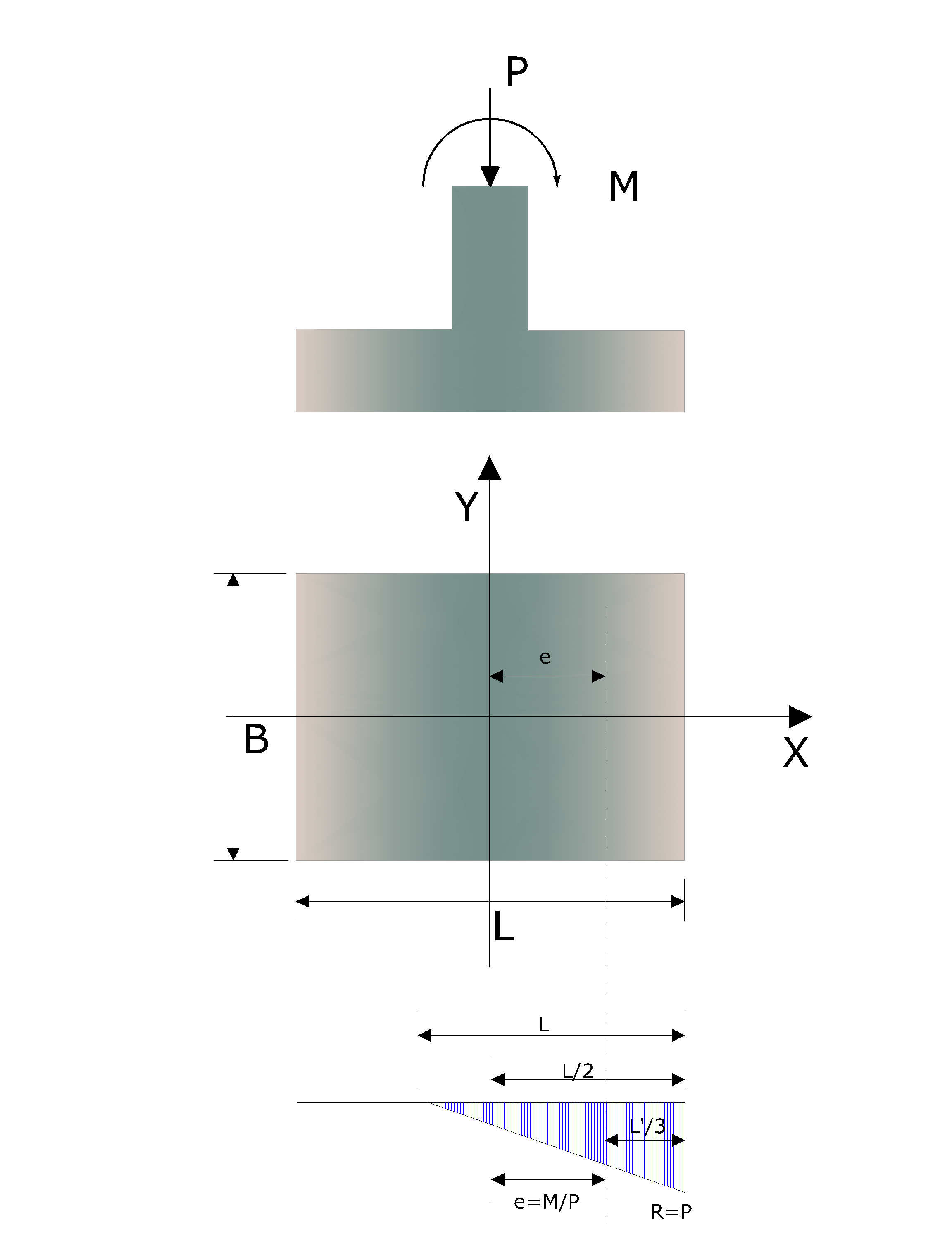
Pressure diagram when e>L/6
The area of the triangle of pressures must be equal to the vertical load P and the resultant must be applied at L'/3 of the most stressed edge and pass through the barycenter of the triangle. This point is located at a distance
![]()
from the center of the foundation so
![]()
and
![]()
Substituting L' in the expression of P and solving for q we obtain

With P, q'a and eccentricity e fixed, is solved relating to B and L for attempts until to satisfy the equality.
When the moment is present, related to both x and y axis, the position of the resultant is like the in figure below
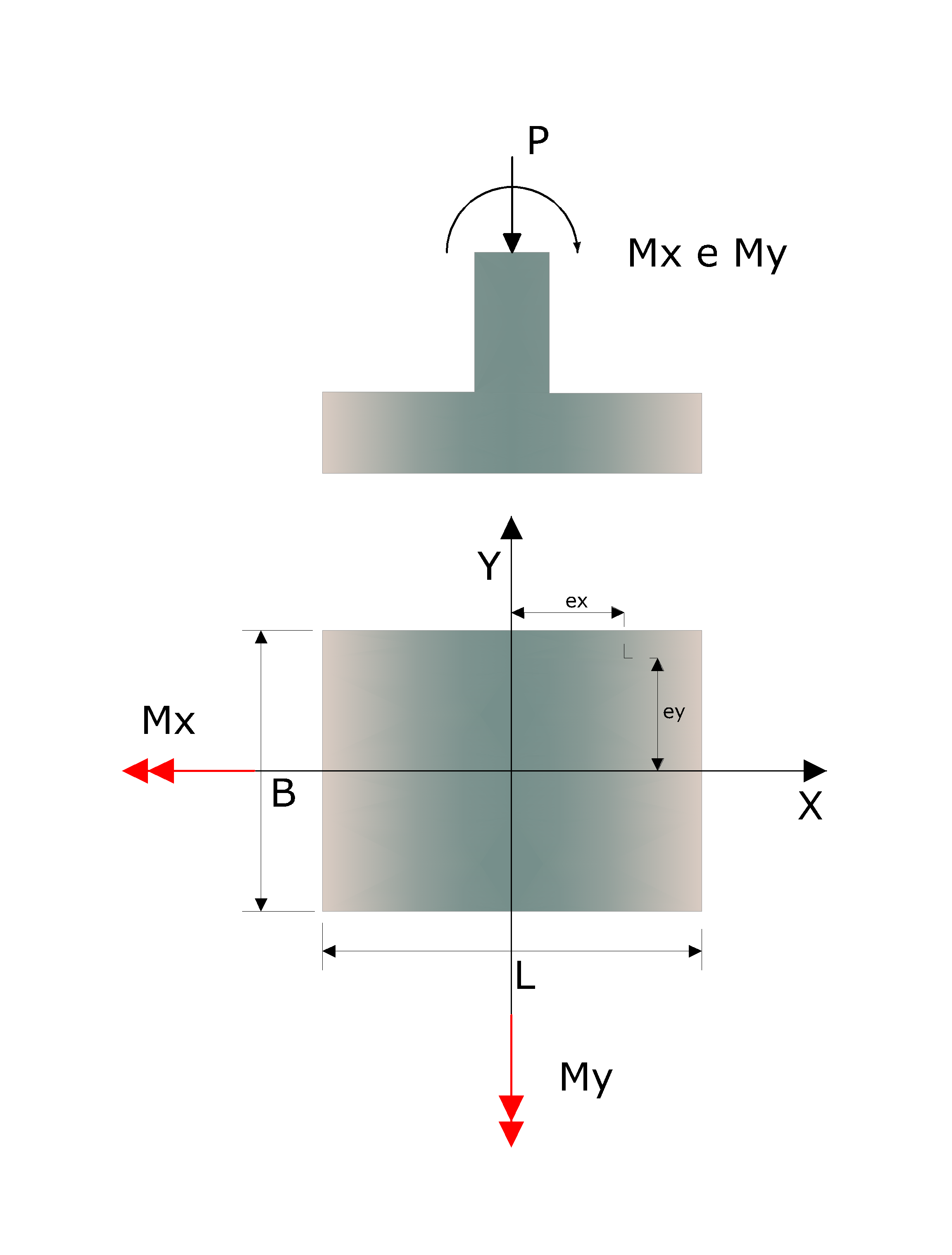
Position of the resultant when we have moment with respect to x and with respect to y
and if both eccentricities are
![]()
![]()
only a part of the foundation is reacting.
The pressure on the soil for foundations with eccentricity regarding both axes can be calculated, when there is no lifting of the foundation from the soil, as follows:

or

We remind that

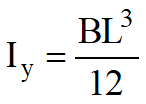
My is the moment regarding the y axis;
Mx is the moment regarding the x axis;

![]()
The positive sides are the ones shown.
In the case of circular foundations the relationships used for the calculation of the maximum contact pressure are:
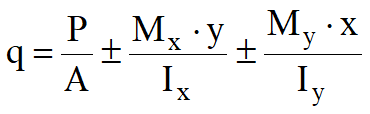
![]()
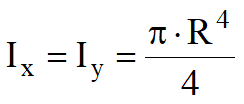
y and x are calculated from the axis center of gravity of the section. Imposing q = 0 is found the position of the neutral axis that allows to calculate the effective area (area reacting to compression) used in the sliding check.
© GeoStru