The vertical bearing capacity of the foundation soil is verified according to the theory of limit states using the following inequality:
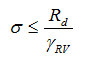
or based on the factor of safety as:
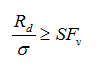
where:
σ-extreme design contact stress at the footing bottom
Rd-design bearing capacity of foundation soil
γRV-coefficient of vertical bearing capacity of foundation
SFv-safety factor for vertical bearing capacity
Extreme design contact stress at the footing bottom is assumed the form:
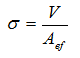
where:
V-extreme design vertical force
Aef-effective area of foundation
Effective Area
When solving the problem of eccentrically loaded foundations the program offers two options to deal with an effective dimension of the foundation area:
•a rectangular shape of effective area is assumed
•circular shape of effective area is assumed
Rectangular shape
A simplified solution is used in such cases. In case of axial eccentricity (bending moment acts in one plane only) the analysis assumes a uniform distribution of contact stress σ applied only over a portion of the foundation l1, which is less by twice the eccentricity e compared to the total length l.
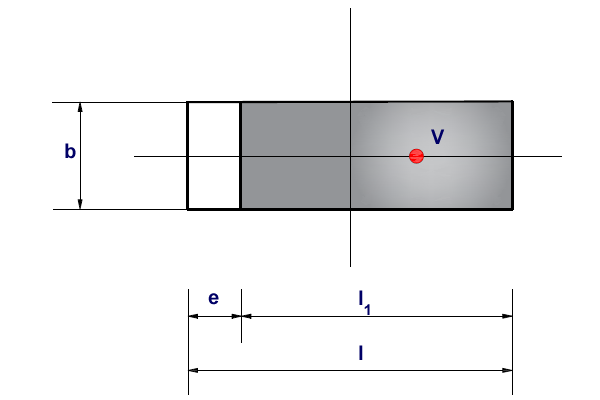
Determination of effective area in case of axial eccentricity
An effective area (b*l1) is assumed to compute the contact stress, so that we have:
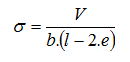
In case of a general eccentric load (foundation is loaded by the vertical force V and by bending moments M1 and M2 the load is replaced by a single force with given eccentricities:
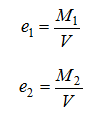
The size of effective area follows from the condition that the force V must act eccentrically:
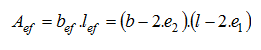
Circular shape
A circular foundation subjected to a vertical load applied with an eccentricity e=Md/Nd can be regarded as an equivalent fictitious foundation with a centrally applied load (Figure), as suggested by Meyerhof (1953) and Vesic (1973). In this case,the area of the fictitious foundation, A', can be calculated as:
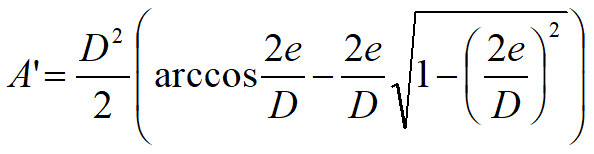
The aspect ratio of the equivalent rectangular area can also be approximated as the ratio of the line lengths b to l, as shown in Figure that is,
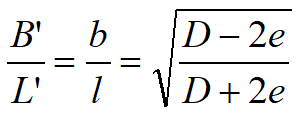
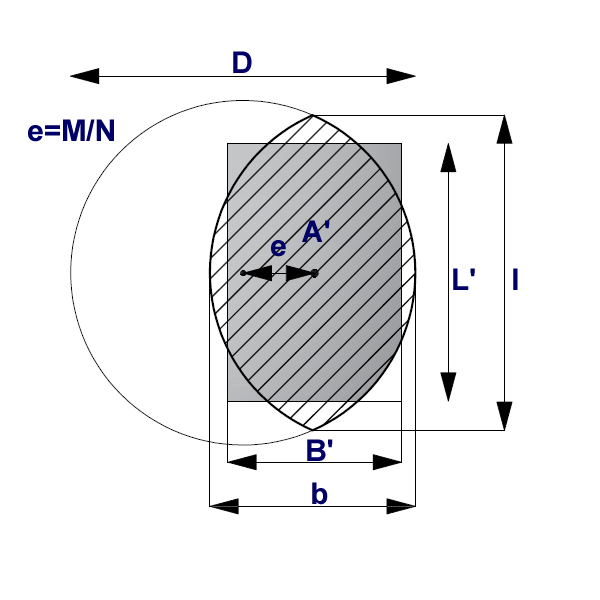
Calculating method of the equivalent dimensions of a circular foundation subjected to a non-barycentric load.
© GeoStru