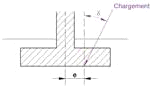
2.5.1 -Coefficienti di riduzione della portanza

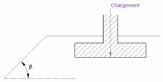
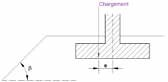
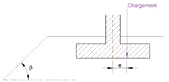
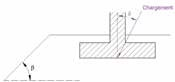
Il calcolo dei coefficienti iδ e iβ è indipendente dalle prove in situ utilizzate (metodo pressiometrico o penetrometrico) per determinare il carico limite netto qnet . Il coefficiente iδ prende in considerazione l'inclinazione del carico considerato, mentre il coefficiente iβ consente di tenere conto dell'effetto di una possibile pendenza in prossimita' della fondazione. In assenza di inclinazione o pendenza (o per un terrapieno situato ad una distanza maggiore di d = 8 B – cf . Figura 9), abbiamo rispettivamente iδ = 1 o iβ = 1.

La tabella 18 riassume i diversi casi possibili e fornisce le espressioni qnet corrispondenti.

2.5.2 - Calcolo del coefficiente iδ

Il valore di calcolo dell'inclinazione del carico rispetto alla verticale è il seguente:

[Formula D.2 .4 (1)]

Con:

Hd: componente orizzontale degli sforzi;

Vd: componente verticale degli sforzi.

iδ è il coefficiente di riduzione della portanza relativo all'inclinazione del carico, è 1,0 se il carico è verticale (Hd = 0).

Altrimenti, viene calcolato in base alla natura del terreno sotto la fondazione come descritto nella tabella 16. Gli abachi dell'allegato B consentono inoltre di determinare iδ dai vari parametri del suolo e delle fondamenta.

Terreno coesivo*		[D.2.4. 1]
Terreno incoerente	Per	[D.2. 4.2]
	Per	[D.2. 4.3]
Terreno coerente e incoerente		con α = 0.6 [D.2. 4.4]
Dopo sviluppo	Per
	Per

Tabella 16: Valutazione del coefficiente di portanza iδ

L'angolo δd è sempre positivo (in valore assoluto), il che significa che i carichi verticali e orizzontali devono sempre essere presi positivamente. Gli angoli δd e Ⴔ ' sono espressi in radianti nelle formule.

2.5.3 - Calcolo del coefficiente iβ

iβ è il coefficiente di riduzione della portanza correlato alla vicinanza di un pendio β , è 1 se la fondazione è sufficientemente lontana dal pendio (d > 8 B).

d: distanza orizzontale dell'angolo inferiore della suola dal pendio;

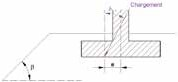
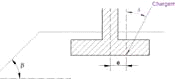
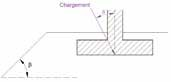
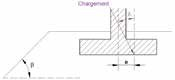
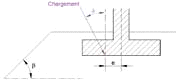
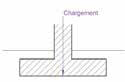
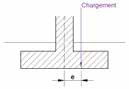
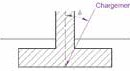
β: inclinazione del pendio (Figura 9).

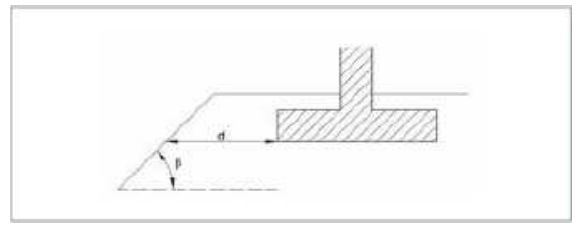
clip0146

Figura 9: Parametri geometrici per il calcolo del vincolo iβ la presenza di un terrapieno

Il coefficiente iβ è calcolato come descritto nella tabella 17 (solo per un angolo di inclinazione inferiore a 45°).

Terreno coesivo*

Per

[Form D.2.5.1]

Terreno incoerente**

Per

[Form D.2.5.2]

Terreno coerente e incoerente

con α = 0.6 [Form D.2.5.3]

* Questa relazione presuppone che la coesione del suolo sia perenne. Questa formula sarà quindi utilizzata principalmente per la giustificazione dei lavori per situazioni di calcolo transitorie. [D.2.5 (3) NOTA 1]

** Per i casi in cui poi iβ è 1 per terreno incoerente.

Table 17: Evaluation of the lift coefficient iβ related to the presence of a slope

2.5.4 -Combinazione dei coefficienti iβ e iδ

In caso di considerazione simultanea di un'inclinazione del carico e della presenza di un pendio, sono possibili due casi:

• L'inclinazione del carico è diretta verso l'esterno del pendio:

• L'inclinazione del carico è diretta verso l'interno del pendio e si può utilizzare la seguente espressione semplificata (34):

La tabella 18 riassume, per ciascuna delle situazioni possibili, le formule di qnet da utilizzare nel caso del metodo pressiometrico (per il metodo penetrometrico, l'approccio è simile sostituendo nelle formule kp con kc e ple* con qce).

Carico verticale

Carico inclinato

Centrato

Eccentrico

Centrato

Eccentrico

Inclinazione del carico

Inclinazione ed eccentricità non opposte

Inclinazione ed eccentricità opposte

Pendio

(a d < 8 B e/o d + De / tan β < 8 B))

Verso l'esterno del pendio