Le strutture ricadenti in zona sismica devono possedere una duttilità coerente con il fattore q di struttura adottato (punto 7.3.6.2 NTC).
Nel caso delle strutture in calcestruzzo la precedente affermazione si traduce nel controllare che la duttilità in curvatura μφ nelle zone critiche di travi, pilastri e pareti duttili risulti (§ 7.4.4 NTC - §5.2.3.4 EC8):
μf ≥ 1,5 (2q0 - 1) per T1 ≥ TC (7.4.1)NTC/(5.4)EC8
μf ≥ 1,5 [1+2(q0 - 1)] TC/ T1 per T1 < TC
dove:
q0 valore massimo del fattore di struttura
T1 periodo proprio fondamentale della struttura
TC periodo corrispondente all’inizio del tratto ad accelerazione costante dello spettro di progetto
I controlli di cui alle suddette formule si riferiscono alle seguenti sezioni ricadenti in:
| • | zone critche di estremità di tutte le travi (non secondarie) |
| • | zone critiche dei pilastri all'attacco con le strutture di fondazioni (in CDB sono escluse tutte le altre zone critiche dei pilastri poste ai piani superiori al primo) |
| • | zone critiche delle pareti duttili (trattate nel paragrafo duttilità locale pareti) |
Queste condizioni, aggiunge il citato punto delle NTC, potranno ritenersi soddisfatte applicando le regole di progetto specifiche e di gerarchia delle resistenze indicate per le singole categorie costruttive. Quindi nel caso di nuove costruzioni le suddette verifiche di duttilità in pratica non vengono mai utilizzate (esse comporterebbero la costruzione diretta del diagramma momenti-curvature per ogni combinazione di carico sismica) ma si ricorre alle seguenti e più semplici formule.
NTC: la duttilità delle travi viene garantia dalle percentuali limite fornite dalla (7.4.25); per i pilastri dalle (7.4.28) ma queste possono non essere conservative nel caso di sforzo normale elevato e/o fattore struttura elevato; per le pareti duttili si danno solo generiche indicazioni sull'armatura trasversale delle zone confinate di estremità.
EC8: la duttilità delle travi va controllata mediante le (5.11),(5.12)EC8; in classe media di duttilità (DCM) per le sole sezioni di base (all'attacco con le fondazioni) dei pilastri va applicata la (5.15)EC8; in classe di duttilità alta (CDH) la (5.15) va applicata per tutte le zone critiche di tutti i pilastri ma con la riduzione della curvatura (5.4) attuata assumendo q0 = 2/3 di q0 (nessuna riduzione per le sezioni all'attacco con le fondazioni); per le zone critiche delle pareti duttili va applicata invece la (5.20)EC8. Ciò in pratica consente di evitare la verifica della duttilità mediante calcolo diretto a patto di applicare, nel caso delle strutture in c.a., le regole di gerarchia delle resistenze e quelle relative ai dettagli delle armature trasversali (staffe di confinamento ecc.) sia per quantitativo che per disposizione.
In particolare nel caso in cui la sezione, in zona critica con obbligo di verifica, di un pilastro venga calcolata in base all'EC8, il programma applica (selezionando l'appostita casella nei dati generali) la (5.15) EC8:
α wwd ≥ 30 mf nd εsy bc/b0 - 0.035 (5.15) EC8
in cui:
α = αs · αn = efficienza del confinamento definita in dettaglio successivamente in questo stesso paragrafo
wwd = (volume totale staffe/volume nucleo cls) · fyd/fcd = (Ast,x/(s· b0) + Ast,y/(s · h0)) · fyd/fcd = wx + wy
mf è proprio la richiesta duttilità in curvatura della struttura cui appartiene il pilastro di cui alle già esaminate espressioni di cui § 7.4.4 NTC e §5.2.3.4 EC8.
nd = NEd / (Ac fcd) = sforzo normale di combinazione normalizzato
εsy è la deformazione dell'acciaio in corrispondenza della tensione di snervamento
anche questa relazione (come la (7.4.28) NTC) va verificata nelle due direzioni x ed y:
α wwd ≥ 30 mf nd εsy bc/b0 - 0.035
α wwd ≥ 30 mf nd εsy hc/h0 - 0.035
si noti che occorre avere cura di assicurare lo stesso rapporto di armatura trasversale cioè deve essere circa wx = wy .
Poichè il programma opera in flessione deviata e taglio obliquo la suddetta doppia formulazione della (5.15)EC8 viene ridefinita in funzione della sola effettiva direzione y inclinata (mentre wwd è somma di entrambe le quantità di armature trasversali nelle direzioni ortogonali della sezione) dell'asse neutro a rottura e della relativa quantità di armatura trasversale efficace nella sola direzione y:
α wy = (30 mf nd εsy dc/d0 - 0.035) / 2
in cui dc e d0 sono la dimensione trasversale equivalente e la corrispondente dimensione del nucleo confinato ottenuti dalla verifica per taglio biassiale. Quindi il controllo della duttilità locale della sezione viene operata una sola volta dal programma per ognuna delle combinazioni sismiche e non due volte (separatamente per le direzioni degli assi x ed y) per ogni combinazione.
Lo stesso tipo di controllo unidirezionale viene effettuato dal programma se si opera con la (7.4.28) NTC nella quale, va notato, come non compare però la dipendenza dallo sforzo normale e dalla effettiva duttilità in curvatura della struttura (la (7.4.28) è in corso di revisione nell'ambito del prossimo aggiornamento delle NTC).
Nel caso di sezioni appartenenti a strutture esistenti calcolate con metodo non lineare (pushover) la duttilità in curvatura non può più essere calcolata con le precedeni relazioni semplificate (valide solo nel caso di calcolo lineare con fattore di struttura q), ma al suo posto va valutata la capacità di rotazione (dei meccanismi duttili) a partire dalla curvatura ultima (a rottura) e quella di snervamento che, allo stesso tempo, definiscono col loro rapporto la duttilità in curvatura. La strada migliore per dedurre dette curvature è quella del tracciamento del diagramma momenti-curvature a cui è dedicato il seguito del presente paragrafo con particolare riferimento ai pilastri che, a causa dello sforzo normale, sono gli elementi strutturali per i quali è più difficile ottenere una buona duttilità. Si ricorda che la massima domanda di duttilità per i pilastri è richiesta nelle sezioni di attacco con le fondazioni in cui il modello di comportamento sismico prevede la formazione di cerniere plastiche; nelle altre zone critiche la richiesta di duttilità è inferiore (non dovrebbero formarsi cerniere plastiche grazie al rispetto della gerarchia delle resistenze) e, per tali zone, l'EC8 non richiede specifiche verifiche in classe DCM (per classe DCH richiede ugualmente verifiche di duttilità ma con domanda ridotta). Le NTC richiedono sempre, per tutte le sezioni critiche (alla base ed in elevazione) una minima quantità di staffe di confinamento senza tuttavia commisurarle allo sforzo normale e al fattore di struttura come dovrebbe essere (è in corso la revisione di questa carente norma italiana).
La duttilità di curvatura μf viene così definita nelle NTC (§ 7.4.4 NTC):
“La duttilità di curvatura μf può essere calcolata come rapporto tra la curvatura cui corrisponde una riduzione del 15% della massima resistenza a flessione ovvero il raggiungimento delle deformazioni ultime del calcestruzzo εcu o dell’acciaio εuk e la curvatura al limite di snervamento”.
Né le NTC né l'EC8 forniscono dettagli sia sul significato della precedente definizione né sulle modalità operative con cui condurre il calcolo della suddetta duttilità. Nel seguito si farà riferimento alla letteratura specializzata ed alla prima bozza dell’Eurocodice 8.
Per una valutazione esauriente del comportamento duttile di una sezione soggetta ad uno sforzo normale costante N occorre tracciarne il diagramma momenti curvature utilizzando i legami tensioni-deformazioni basati sui valori medi di resistenza (non quelli di progetto utilizzati per il calcolo di verifica) del calcestruzzo e dell’acciaio.
Si consideri la sezione (30x50) di un pilastro (in figura) insieme al suo diagramma Momenti-Curvature (per N=40000 daN) ottenuto sulla base dei diagrammi medi del conglomerato (parabola-rettangolo con fck=200 daN/cm², fcm =280 daN/cm² ed εcu=0.0035) e dell’acciaio. Il rapporto tra la curvatura a rottura (0.0003088) e quella a snervamento (0.0000781) fornisce il seguente valore della duttilità μf = 3.954.
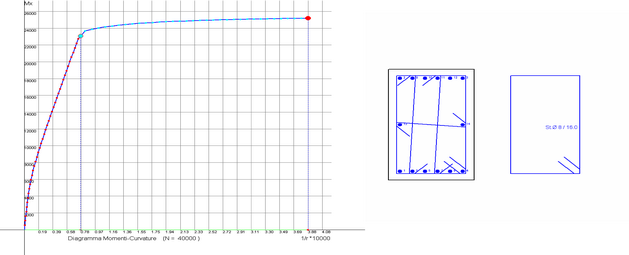
La duttilità così ottenuta è palesemente insoddisfacente per una struttura in zona sismica calcolata ad esempio con un fattore di struttura q0=3.5; infatti dalle norme (§ 7.4.4 NTC) è richiesta una duttilità μf ≥ 2 × 3.5 - 1 = 6.0.
Non potendo ridurre lo sforzo normale (per N=0 ad esempio si otterrebbe μφ = 8,6) l’unico fattore che può migliorare la duttilità è l’incremento della deformazione unitaria ultima del calcestruzzo, che può essere conseguito a mezzo di una fitta staffatura di confinamento. Infatti l’incremento della pressione di confinamento esercitata dalle staffe sul nucleo di calcestruzzo produce un aumento della resistenza e delle massime deformazioni εc0 ed εcu del calcestruzzo stesso. La figura seguente mostra due diagrammi tensioni deformazioni di uno stesso calcestruzzo: quello con tensione massima riferito al calcestruzzo non confinato (tipicamente quello esterno al perimetro delle staffe), quello con tensione massima fck,c è invece riferito al calcestruzzo confinato caratterizzato oltre che da un valore maggiore di resistenza anche da deformazione ultima εcu,c ed al picco della parabola εc0,c molto superiori a quella precedente. La legge costitutiva del calcestruzzo confinato illustrata nella figura seguente trae origine dal modello di Kent-Park ed è caratterizzata dal ramo rettilineo discendente del diagramma che varia in funzione del grado di confinamento.
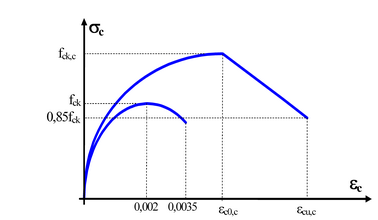
Le principali variabili che determinano l’effetto di cerchiatura evidenziato in figura sono:
| - | il rapporto tra il volume delle staffe e il volume del calcestruzzo racchiuso dalle stesse (ad elevate quantità di acciaio corrispondono elevate pressioni di confinamento); |
| - | la tensione di snervamento dell’acciaio delle staffe in quanto fornisce un limite superiore alla pressione di confinamento esplicabile; |
| - | il passo delle staffe il cui aumento riduce l’effetto arco della pressione di confinamento; |
| - | il rapporto tra il diametro della barra della staffa e la lunghezza del lato maggiore della staffa, a causa della rigidezza flessionale che la barra gioca nel suo piano per poter sviluppare la pressione di confinamento (questo problema non è presente nei pilastri circolari mentre per quelli rettangolari viene risolto mediante legature trasversali che collegano le barre longitudinali ed al tempo stesso le staffe chiuse perimetrali). |
Nel programma è possibile definire contemporaneamente, nei dati dei calcestruzzi presenti nell'archivio materiali, i punti rappresentativi dei due diagrammi tensioni-deformazioni attraverso i seguenti valori assegnati nell’archivio stesso:
| - | fck resistenza caratteristica del calcestruzzo non confinato |
| - | fck,c resistenza caratteristica del calcestruzzo confinato |
| - | εc0,c deformazione alla massima resistenza del calcestruzzo confinato |
| - | εcu,c deformazione ultima del calcestruzzo confinato |
Il suddetto diagramma è tratto dalla prima versione dell'EC8. Oggi si ritiene più corretto operare con i valori medi fcm, fcm,c delle resistenze (il valore fcm è assegnabile direttamente nell'archivio materiali). I valori εc0 ed εcu del calcestruzzo non confinato non vanno assegnati nell’archivio in quanto calcolati automaticamente dal programma.
Per la precedente sezione la seguente quantità di staffe (in zona critica) ottenute dalla (7.4.28) del § 7.4.6.2.2 NTC in classe di duttilità “CDB” dovrebbe da sola (senza calcolo diretto) garantire la richiesta duttilità in curvatura:
Ast/s ≥ 0.08 · bst · fcd / fyd (7.4.28) NTC
In cui s è il passo delle staffe, bst è la distanza tra i bracci più esterni delle staffe. La formula va applicata per entrambe le direzioni degli assi della sezione (supposta sempre rettangolare) potendosi così riscrivere:
wx = Ast,x /(s · b0) · fyd / fcd ≥ 0.08
wy = Ast,x /(s · h0) · fyd / fcd ≥ 0.08
quindi in definitiva deve essere
w = wx + wx ≥ 0.16
In "CDA" il coeff. 0.08 va sostituito con 0.12.
Utilizzando un calcestruzzo di classe C20/25 ed un acciaio B450C si ottiene come area minima di staffe al metro (s=100cm):
Ast = 100 × 0,08 × 113,3 × 44 × 3913 = 10,19 cm²/m
Utilizzando staffe Φ 8 a 2 bracci per soddisfare l’area minima di staffe occorrerebbe un passo s = 10,19/1,005 = 10,1 cm che soddisfa sia il passo minimo assoluto fissato in 17,5 cm sia il passo minimo funzione del diametro delle barre longitudinali e pari ad 8 volte tale diametro (che vale s= 8 × 1,4 = 11,2 cm).
Avendo pertanto adottato staffe Φ 8 a 2 bracci con passo 10,1 cm si vuole ora determinare il valore dei punti caratteristici del calcestruzzo confinato. Per prima cosa va determinata la pressione di confinamento laterale σ2 con la seguente formula sperimentale:
σ2 = 0,5 fck αs αn ωw
dove:
ωw = (volume staffe chiuse conf. / volume calcestruzzo conf.) · fyk/fck
αs = (1-s/2b0)(1-s/2h0) in cui b0 , h0 sono i lati del nucleo confinato misurato dall'asse della staffa perimetrale [formula (5.17a) EC8]
αn = 1- ∑bi2/(6⋅b0⋅h0) in la sommatoria è riferita alle distanze bi tra le barre longitudinali consecutive collegate dalle staffe o dalle legature [formula (5.16a) EC8]
αs αn e ωw sono quelli indicati esplicitamente nell’Eurocodice 8. Per una generica sezione poligonale αs = Ac/A0 dove A0 è l'area racchiusa dall'asse della staffa perimetrale e Ac è l'area del poligono interno ad A0 ottenuto con un offset dei lati di A0 pari a di s/4. Sempre per una sezione poligonale nella formula di αn il prodotto b0⋅h0 va sostituito con l'area A0 appena definita.
Nella sezione illustrata nella prima figura del paragrafo ed avente dimensioni di 30×50 con copriferro, misurato dal baricentro delle barre longitudinali, di 4.5 cm, si ha un nucleo confinato di b0 × h0 pari a 23,4×43,4 cm , inoltre:
ωw = 67,15 / (23,4 × 43,4 × 10,1) × 4500/200 = 0.147
αs = (1- 10,1/(2 × 23,4)(1-10,1/(2 × 43,4) = 0.693
αn = 0,733
σ2 = 0,5 × 200 × 0,693 × 0,733 × 0,147 = 7.47 daN/cm²
Una volta nota la pressione σ2 laterale efficace del calcestruzzo dovuta al confinamento possono applicarsi le formule (3.24), (3.25), (3.26), (3.27) dell’EC2 che forniscono i cercati parametri di tensione e deformazione del calcestruzzo confinato:
fck,c = fck (1,000 +5,0 σ2/fck) per σ2 ≤ 0,05 fck
fck,c = fck (1,125 +2,5 σ2/fck) per σ2 > 0,05 fck
fcu,c = 0,85 fck
εc0,c = εc0 (fck,c/ fck)²
εcu,c = εcu + 0,1 × αs × αn × ωw
Nel nostro caso risultando σ2 < 0,05 fck = 10 daN/cm² si ha:
fck,c = 200 (1.000 + 5.0 × 7.47/200) = 237.3 daN/cm²
fcu,c = 0.85 × 200 = 170 daN/cm²
εc0,c = 0.002 (237.3/ 200)² = 0.00282
εcu,c = 0.0035 + 0.1 × 0.693 × 0.733 × 0.147 = 0,0109
Il calcolo è stato effettuato con i valori caratteristici di resistenza ma andrebbe più correttamente effettuato con i valori medi (con un ulteriore incremento di duttilità di curvatura).
Si noti l’enorme aumento, grazie alle staffe, della deformazione ultima del calcestruzzo confinato (oltre 3 volte quello non confinato) che conferisce allo stesso una notevole duttilità che in definitiva consente alla sezione curvature plastiche di entità molto superiori a quelle ottenibili senza confinamento.
Per valutare il conseguente incremento della duttilità in curvatura μφ è necessario rielaborare il diagramma momenti-curvature assegnando nell'archivio materiali i parametri di tensione e deformazione sopra calcolati e tenendo conto nel calcolo del differente legame costitutivo relativo al nucleo di calcestruzzo confinato b0, h0 rispetto a quello del calcestruzzo esterno (copriferro). Si ottiene così il diagramma in figura dal quale si deduce il valore della duttilità di curvatura che qui risulta pari a μφ = 13,53 e, quindi, questa volta in grado di rispettare sicuramente la prescrizione normativa.
Si noti il brusco calo del momento resistente che denota la rottura del copriferro non confinato (col conseguente annullamento della sua resistenza) e l’andamento successivo leggermente decrescente del diagramma dovuto al tratto decrescente del diagramma tensioni deformazioni del calcestruzzo confinato. Nel caso in cui tale momento decrescente dovesse comportare una riduzione superiore al 15% del momento massimo, il valore di curvatura da assumere per il calcolo della duttilità di curvatura dovrebbe essere quello corrispondente all’85% del momento massimo e non quello ultimo a rottura.
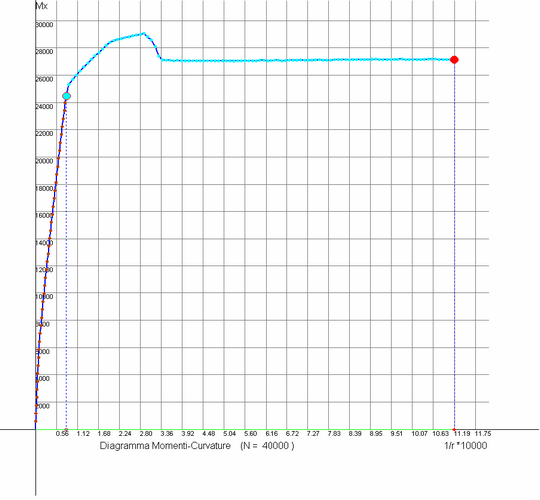
Quest’ultima considerazione spiega compiutamente il significato della definizione di duttilità in curvatura di cui al punto 7.4.4 NTC.
Il differente colore dei punti del diagramma momenti curvature é dovuto al fatto che nel tratto iniziale ad andamento quasi lineare, con forte pendenza, i punti del diagramma vengono costruiti incrementando il momento flettente (calcolo in controllo di forza); successivamente (dopo il raggiungimento del momento di snervamento) i punti vengono dedotti incrementando a passo costante la curvatura (calcolo in controllo di spostamento).
Il programma consente anche la determinazione del diagramma momenti-curvature e della duttilità mediante calcolo automatico dei parametri del legame costitutivo del calcestruzzo confinato sulla base delle staffe effettivamente assegnate alla sezione: in questo caso i valori dei parametri del diagramma parabola-trapezio presenti nell'archivio materiali non vengono utilizzati nel calcolo. Ciò agevola notevolmente il calcolo ma che può essere eseguito solo per per sezioni di forma generica costituite da un solo dominio poligonale, nonchè per tutte le sezioni predefinite per i pilastri a sezione rettangolare e per le pareti. Per semplicità il tratto lineare decrescente del diagramma costitutivo del calcestruzzo termina (in corrispondenza della deformazione ultima) con un valore convenzionale pari all'85% della resistenza del calcestruzzo non confinato (senza porlo in diretta dipendenza della effettiva quantità di staffe confinanti).
Nel caso di presso-tenso flessione deviata il programma opera la determinazione del diagramma momenti-curvature x-curvature y mantenendo costante, per ogni punto del dominio, oltre allo sforzo normale N, il rapporto Mx/My assegnato in combinazione. Tutti i valori calcolati (delle componenti di curvatura e dei momenti) vengono visualizzati a video e possono essere stampati. Nella rappresentazione grafica viene però rappresentata la sola somma vettoriale delle componenti delle curvature e dei momenti.
Il programma prevede un’ulteriore tipo di diagramma tensioni-deformazioni che descrive il comportamento deformativo della sezione da impiegare ad esempio nel calcolo non lineare non sismico dei telai. In questo caso viene assunto automaticamente nel calcolo il diagramma tensioni deformazioni descritto nel § 3.1.5 dell’EC2 che è caratterizzato da una tensione massima fcm (picco parabola) pari a fcm = fck+80 [daN/cm²] e da deformazioni ec0 ed ecu molto prossime a quelle impiegate nel calcolo di resistenza. Come modulo elastico secante all’origine Ecm viene assunto quello assegnato nell’archivio dei materiali. E’ possibile assegnare nella finestra dei dati generali della sezione la % p della resistenza a trazione media fctm da prendere in conto nel calcolo della resistenza a trazione del calcestruzzo (tension stiffening) indicata nel diagramma tensioni-deformazioni del calcestruzzo. L’andamento in trazione del diagramma è lineare con pendenza Ecm (uguale a quella in compressione), fino al raggiungimento di p· fctm , per poi decrescere, sempre linearmente, fino alla tensione nulla in corrispondenza della deformazione unitaria di -0,007.
Ponendo nulla la percentuale p si opera comunque in favore di sicurezza (trascurando il tension stiffening gli sforzi e le deformazioni aumentano). Nella figura seguente è rappresentato il diagramma di cui trattasi ottenuto col 100% di fctm.
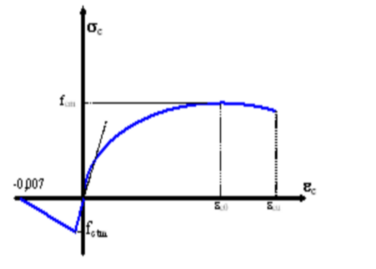
Anche per questo diagramma momenti curvature è previsto il calcolo in presso flessione deviata con la determinazione per ogni punto delle componenti di curvatura relative ad entrambi gli assi principali d’inerzia della sezione di solo conglomerato.

|
© 2013 Geostru Software