PERMANENT MOTION STATE HYDRAULICAL VERIFICATION
The permanent motion with gradual variations flowing is that which is occurs in a free current with gradual variations in the beds cross section. continuity determines that capacity is constant, while velocity and cross section vary gradually along the flow’s s axis.
If we consider a permanent flowing current with a minor inclination and a constant Q flow, isolating a riverbed section with ads length (with the s abscissa measured from a point that was not previously calculated, in the horizontal direction towards the coincident with the flowing point) the depth is being subsided with if ds and the total load line withJds , indicating the fall with J.
From simple geometrical considerations we have:
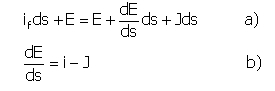
The expression b), in which for simplicity if was specified with as being equal to i, it indicates the total specific energy that refers to the depth, grows by the depth’s subside and is diminutions through the resistance effect.
Substituting the finite growth differences b) becomes:
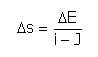
E results depending on s, through the h height we have:
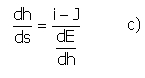
From E' s displacement depending on h, we know that E is decreasing and increasing in function of h (dE/dh < 0) for rapid currents (h < k), and is increasing (dE/dh > 0) for lent currents (h > k); in function of the critical state dE/dh = 0.
Accepting for the charge loss J the following formula:
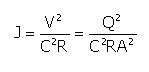
results that J is as decreased as h is increased, assuming that all the dinominater's terms are increasing with h.
c)'s numerator is positive (i > J) for water heights that surpass those of the uniform flow (h > h0), negative for water heights that no not surpass those of the uniform flow(h < h0).
The considerations made until now are at the base of the water profile's permanent flow represents: we note that when the water height is approaches that of the uniform flow, dh/ds tends to zero, or the profile tends to lie parallel to the bed and to the uniform flow.
But when the height is tending to the critical value k, dE/dh tends to be annulated so the profile tends to be displayed perpendicularly on the base (depth).
So the permanent flow profiles are analytically described by the expression b), so specify at least one arbitrary constant to determine by defining a section's height like this h = h*.
Such a condition is calculated in function of a perturbatory cause that provokes, in a section, a height h different from that of the uniform flow; for this purpose the perturbatory cause can have influence uphill only if the current is slow (or becomes slow), it can have influence downhill only if the current is a fast one (or it becomes rapid because of this influence).
All these get to the conclusion that the profile's relation - the displacement's depart point - is found downhill if the current is slow and uphill if the current is fast.
In such a section we have to note the height h* determined as the cause of perturbation and the level difference h*- h0 will be known in reference to uniform flow.