Il metodo di Westergaard è un metodo che serve per la soluzione dell’equazione di Lagrange per le lastre sottili. Da un punto di vista generale il metodo è quindi uno strumento per il calcolo della massima deflessione cui è soggetta una lastra sottile stratificata (alla quale viene approssimata la pavimentazione stradale). Il criterio di verifica (o progetto) è analogo a quello sul quale si basa il metodo della massima deflessione. In generale la misura dell’adeguatezza di una pavimentazione stradale è espressa attraverso la seguente misura di sicurezza:

Dove fadm è la deflessione ammissibile che la strada è in grado di sopportare nella vita utile della strada, mentre fd è la deflessione calcolata sulla strada di progetto.
IL CALCOLO DELLA DEFLESSIONE DI PROGETTO
Ai fini del calcolo della deflessione di progetto si consideri un generico piccolo elemento all'interno di un generico strato della sovrastruttura:
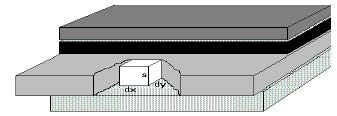
Figura 1 – Generico elementi all'interno della pavimentazione
Nell'ipotesi che gli strati si possano considerare omogenei, isotropi ed elastici e che lo strato sottostante reagisca verticalmente ed in modo proporzionale al cedimento, l'equazione di Lagrange fornisce l'equazione di equilibrio indefinito per un generico elemento infinitesimo dello strato sottile, che descrive la componente dello spostamento w ortogonale al piano medio dello strato:
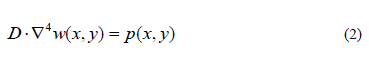
Nella quale:

Con:
•p: Carico esterno sull'elemento infinitesimo;
•D: Coefficiente di rigidezza flessionale;
•s: Spessore dello strato;
•E: Modulo di Young dello strato;
•n: Coefficiente di Poisson dello strato.
L'equazione (2) è scritta con riferimento alle convenzioni mostrate nella seguente figura:
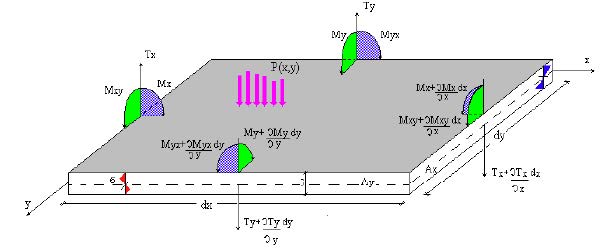
Figura 2 – Convenzioni utilizzate per la scrittura della equazione
(2)
La (2) è stata scritta nel caso generale di una piastra soggetta ad un carico p(x,y) e a delle azioni di bordo M, F.
Nel caso stradale Westergaard ha modificato la (2) esprimendo il carico p(x,y) come somma di due contributi: uno dovuto ai carichi applicati sulla faccia superiore dello strato g(x,y) che rappresentano i carichi veicolari, l'altro dovuto alla reazione del piano di posa applicato sulla faccia inferiore q(x,y). Westergaard ha assunto questa componente proporzionale al cedimento nella seguente forma:
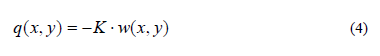
Dove K è un coefficiente di proporzionalità che assume il significato di modulo di reazione del piano di posa. Le esperienze di Westergaard hanno descritto in modo preciso le modalità sperimentali per la determinazione di tale parametro. Introducendo la (4) nella (2) è possibile scrivere quanto segue:
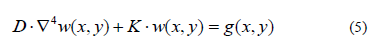
Per la soluzione di questa equazione Westergaard ha proposto i impiegare le serie doppie di Fourier. Si consideri quindi il comportamento della piastra sotto un carico di tipo sinusoidale del tipo:
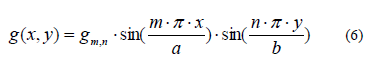
Alla luce della (6) è abbastanza semplice verificare che l'equazione (5) è soddisfatta da una funzione w(x,y) della forma seguente:
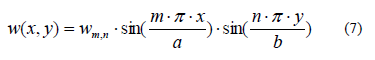
Nelle equazioni (6) e (7) a e b rappresentano rispettivamente le lunghezze del lato parallelo ad x e del lato parallelo ad y della lastra applicata. Wm,n può essere calcolato sviluppando i necessari calcoli. A vantaggio di chiarezza si espone direttamente quello che è il risultato dei calcoli di cui sopra:
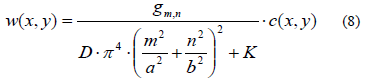
Dove:
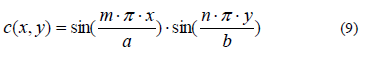
A questo punto si introducono le serie doppie di Fourier, attraverso le quali è possibile formulare una decomposizione di una qualunque distribuzione di carico ga(x,y) attraverso uno sviluppo in serie del tipo:
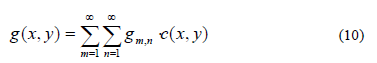
Dove c è definito dalla (9). Affinchè la (10) sia valida gm,n deve essere calcolata mediante la seguente formula:
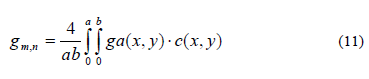
Ciascun termine della (10) soddisfa la (5) e le condizioni al contorno e per la sovrapponibilità degli effetti sommando tutte le w(x,y), si ottiene la funzione della superficie elastica deformata del piano medio soggetta al carico assegnato ga(x,y)
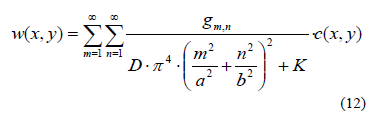
Nota la w(x,y) è possibile ricavare gli sforzi e le componenti di azione interna (oltre che le deformazioni). A questo punto sono noti esattamente i cedimenti della lastra da cui si può ricavare la reazione in ogni punto dello strato sottostante. Questa rappresenterà il carico ga(x,y) che verrà applicato allo strato inferiore per ripetere il calcolo nell’ipotesi che il piano di posa sui poggia reagisca con un modulo di reazione K1 (in generale diverso da K). La procedura può essere ripetuta per tutti gli strati pervenendo così alla soluzione in ciascun punto di qualunque strato.
IL CALCOLO FADM
Il calcolo della deflessione ammissibile si determina invece mediante la seguente formula:
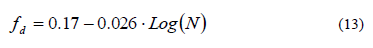
Nella espressione (13) N è il numero di assi equivalenti a quello standard che transiteranno sulla strada nell’ultimo anno di vita utile in un giorno per la corsia di progetto.
© Geostru
>