Before performing a local seismic response analysis, it is possible to define a set of monitored nodes, at which the results of the analysis will be returned. The advantage of assigning monitored nodes is a considerable reduction in calculation time, as the local seismic response will only be returned with reference to these nodes and not for the entire domain. To select a monitored node, in the Tools panel, after selecting the node, simply click on the ‘Add Monitored Nodes’ button in the top bar.

The monitored nodes are highlighted as shown in the figure above.
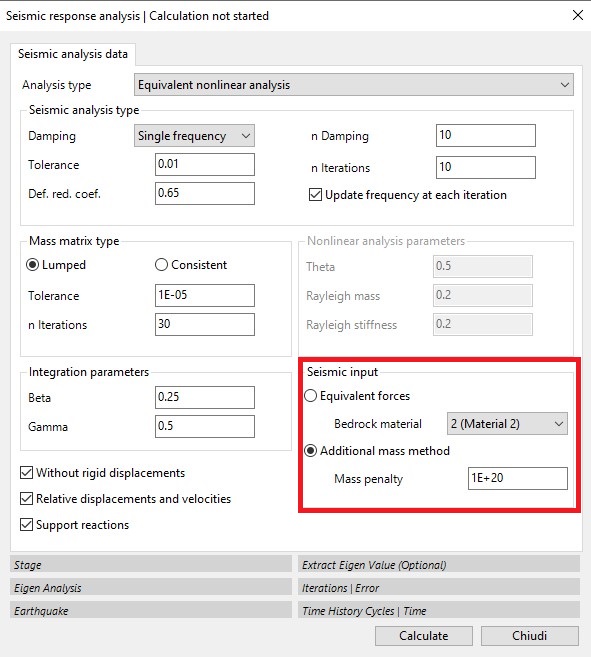
To perform the local seismic response analysis, it is necessary to use the ‘Seismic Response Analysis’ button in the Analysis and Results panel. This command will result in the window shown below.

Several analysis options can be selected in this window, including:
a) No rigid displacements
b) Relative displacements and velocities
Option (a) does not consider the absolute rigid displacement of the system in the dynamic analysis. Generally, this option should be selected as rigid displacements cause no additional stresses.
Selecting option (b) returns the relative displacement for each node at the end of the calculation, otherwise the displacement returned is the absolute displacement.
Dati analisi sismica
RSL III 2D software allows four types of analysis:
▪Equivalent non-linear analysis
▪Linear analysis with variable damping
▪Linear analysis with constant damping
▪Dynamic analysis
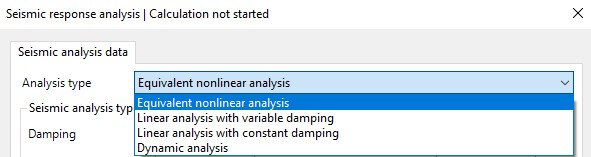
Possible types of analysis in RSL III 2D
From a theoretical point of view, the dynamic analysis for a finite number of nodes is performed by solving a system of equations of the type:
![]()
where
[M] = mass matrix
[C] = damping matrix
[K] = stiffness matrix
R = vector of known loads equal to [M]ag with ag input accelerogram.
u is the vector of relative displacements.
The system is solved in the time domain according to Newmark's principle: it consists of a series of successive integrations, for each step Δt, to determine the velocity and thus the relative displacement u. In the application of Newton's method, certain integration parameters are required (red box in the following figure).

Beta and Gamma are two parameters of the Newmark integration method that generally have values of 0.25 and 0.5, respectively.
Soil damping is accounted for through the matrix [C]. For each element i into which the domain is divided, Ci is calculated according to the Rayleigh criterion, which is correlated with mass and stiffness:
Ci=α∙Mi+β∙Ki
Where α and β are two coefficients called, respectively, Rayleigh mass and Rayleigh stiffness, while Mi and Ki are the mass and stiffness of the individual element. Using this formulation, the damping λ (or damping ratio) can be made dependent on the circular frequency according to the following relationship:
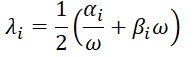
where α and β for the i-th element are calculated as follows:
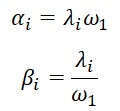
with ω1 the main frequency corresponding to the first vibration mode.
Linear analysis with constant damping (red box in the figure below): the software performs the calculation using Rayleigh's consistent damping matrix with α and β constant for all nodes and equal to the values given in Rayleigh Mass and Rayleigh Stiffness.
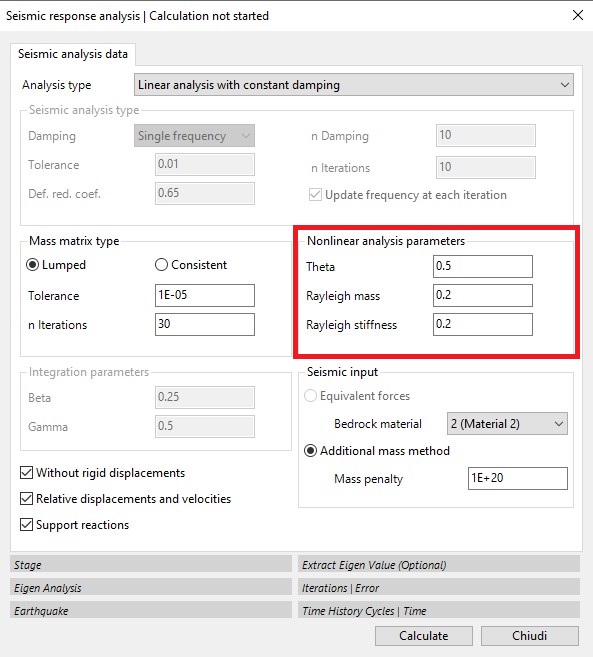
Theta is an integration parameter generally set at 0.5
Linear variable damping analysis: the software performs the calculation using the parameters defined in the material grid as the damping parameters.
Non-linear equivalent analysis (red box in the following image).
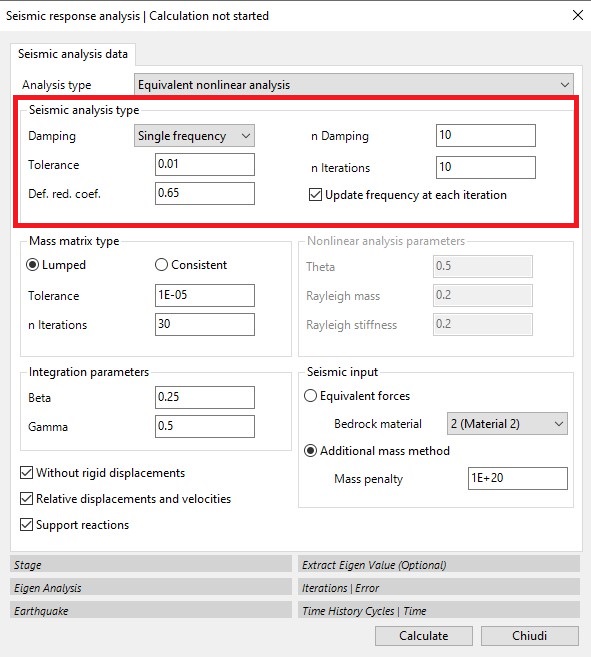
In this case, the software performs a sequence of linear analyses in which the stiffness and damping parameters are updated iteratively until a convergence factor is reached. The calculation begins with the initial values of G and D entered in the material window, and the shear deformation linked to the displacement value u is determined. In each iteration, the values of D and G/Gmax are updated according to the level of effective deformation reached, and the calculation stops when the difference in the values of G and D between one iteration and the next is less than the tolerance level set by the user.
For this type of analysis, users may also choose to update the circular frequency ω at each iteration. This implies that the calculation of the Rayleigh coefficients α and β in the damping matrix C are updated at each iteration for each element as a function of the main frequency ω1, in the case of Single Frequency, or of ω1 and ω2 in the case of Dual Frequency. For each element, in the case of Dual Frequency, the expressions of α and β are:
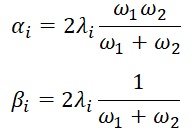
with ω1 the principal frequency and ω2 = nDamp x ω1 , con nDamp with nDamp generally set equal to 10. Basically, for each iteration the average shear strain is calculated for each element and the damping curve is consulted to update the correct value of the damping.
Tolerance defines the deviation between the values of G and D, found between one iteration and the next, which determines the end of the iterative calculation.
The number of iterations determines how many iterations must be performed by the programme: a high number of iterations (>10) results in an unnecessary increase in calculation time.
Coeff. Red. Def. This is a coefficient that reduces the maximum deformation; its value is usually set at 0.65. It is calculated from the following expression: γeff/γmax = (M-1)/10
Other parameters of the equivalent non-linear analysis relate to the modal finite element analysis in which the mass matrix (red box) must be defined:
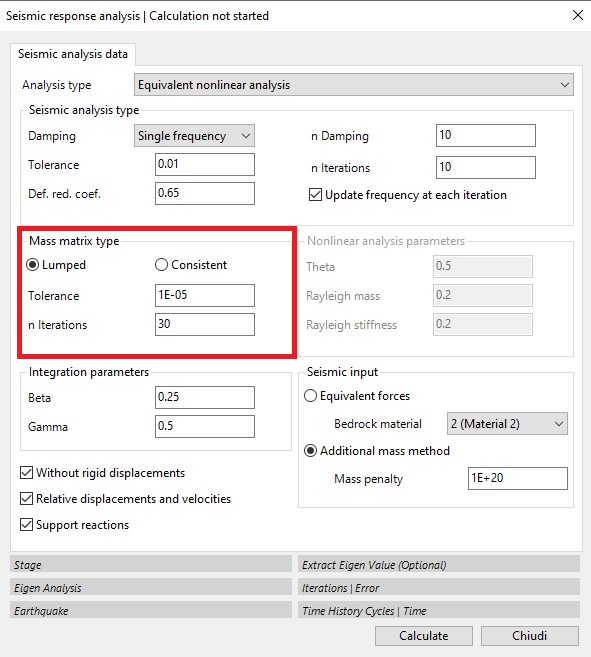
Point mass: the mass is considered to be concentrated at the nodes.
In this case, the structure of the mass matrix is diagonal and offers significant advantages in terms of reduced memory usage and a substantial decrease in computation time. Usually, this assumption does not result in large errors and is therefore preferable.
Consistent mass: the mass is distributed, and the corresponding matrix is essentially full and symmetric. This assumption produces smaller absolute errors but results in an increase in computation time.
Modal analysis parameters: For modal analysis, a tolerance factor must be set, which determines when the calculation should stop, and a number of iterations. If the calculation reaches the set number of iterations, it will stop even if the desired tolerance has not been reached. The modal analysis must be performed for all the nodes in the domain, so it is not carried out by the software when monitored nodes are present.
Seismic input
In performing the RSL III 2D calculation, it is possible to choose between two different methodologies: Equivalent forces and the Additional mass method.
With the first approach, the seismic input is defined in terms of equivalent nodal forces (or effective seismic forces), which are proportional to the velocity of the incident wave and are applied horizontally along the base of the domain defined by the model. This type of seismic input (outcrop input) is considered as a time-varying shear force:
F(t) = ρVsAv(t)
Where ρ is the density of the bedrock, Vs represents the velocity of the S-waves in the bedrock, v(t) represents the velocity of the earthquake, and A represents the area contribution associated with the loaded node.
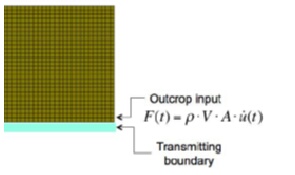
Seismic input using the Equivalent Forces approach
These forces are automatically calculated by the software and are applied to the nodes of the domain in contact with the bedrock. The advantage of this method is precisely that there is no need to model the bedrock layer, but only to select the material it is made of. When selecting this method, the boundary conditions in Phase 1 are represented by springs, both horizontally and vertically, for all boundary nodes of the domain. In Phase 2, the software automatically calculates the spring reactions for all domain boundaries.
©GeoStru