La procedura di calcolo adoperata da RSL per la valutazione della funzione di trasferimento presuppone come base di partenza uno o più accelerogrammi e la conoscenza della stratigrafia del sito attraverso i seguenti parametri geotecnici per ogni strato:
•peso per unità di volume;
•velocità di propagazione delle onde di taglio;
•coefficiente di spinta laterale;
•modulo di taglio iniziale (opzionale);
•spessore;
•indice di plasticità.
La non linearità del calcolo è introdotta dalla dipendenza del modulo di deformazione al taglio e del coefficiente di smorzamento viscoso dalla deformazione.
Schematicamente la procedura è riassumibile nel seguente modo:
1.Valutazione dello spettro di Fourier dell'accelerogramma (omessa nel caso si debba analizzare uno spettro);
2.Ricerca di un errore relativo piccolo seguendo la procedura di:
2.1. Stima della funzione di trasferimento;
2.2. Valutazione della deformazione indotta in ciascuno strato;
2.3. Correzione del modulo di deformazione al taglio e del coefficiente di smorzamento viscoso per ogni strato;
Le operazioni 2.1, 2.2 e 2.3 sono ripetute fino a quando la differenza di deformazione tra un'iterazione e la precedente non rimane al di sotto di una soglia ritenuta accettabile;
3.Trasformazione inversa di Fourier dello spettro precedentemente calcolato ed opportunamente pesato per mezzo della funzione di trasferimento calcolata.
Attraverso questa procedura è possibile "trasferire" l'accelerogramma dal bedrock in superficie. La deformazione per ciascuno strato viene corretta sulla base del rapporto fra deformazione effettiva e massima come suggerito dalla letteratura scientifica, ovvero
dove M rappresenta la magnitudo del sisma.
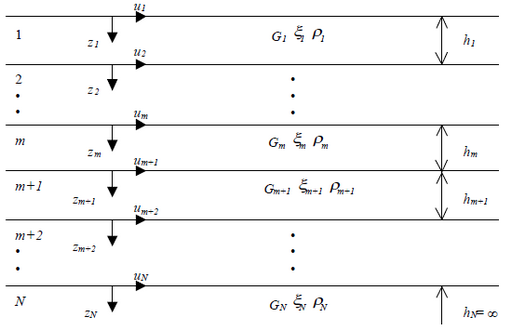
Per la valutazione della funzione di trasferimento, RSL considera un suolo variamente stratificato composto da N strati orizzontali di cui l'N-esimo è il letto di roccia (bedrock). Ponendo come ipotesi che ciascuno strato si comporti come un solido di Kelvin-Voigt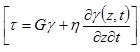 
, la propagazione delle onde di taglio che attraversano gli strati verticalmente può essere definita dall'equazione dell'onda:
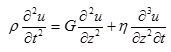(1)
dove: u rappresenta lo spostamento; t il tempo; ρ la densità; G il modulo di deformazione al taglio; η la viscosità. Per onde armoniche lo spostamento può essere scritto come:
(2)
che sostituita nella (1) pone
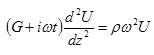(3)
dove w rappresenta la frequenza angolare. La (3) può essere riscritta come
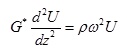(4)
avendo posto 
, ovvero il modulo di deformazione al taglio complesso. Questo può essere ulteriormente riscritto come
(5)
avendo posto
(6)
dove 
rappresenta il coefficiente di smorzamento viscoso. Ciò posto, e fatta convenzione che l'apice * indica la natura complessa della variabili in gioco, la soluzione dell'equazione generica dell'onda è la seguente:
(7)
dove E e F dipendono dalle condizioni al contorno e rappresentano l'ampiezza d'onda che viaggia rispettivamente verso l'alto (-z) e verso il basso (+z), mentre 
rappresenta il numero d'onda complesso dato dalla seguente espressione:
(8)
Il taglio invece è dato da:
(9)
Per il generico strato m di spessore hm gli spostamenti, rispettivamente in sommità (z = 0) ed al fondo (z = hm), sono:
(10)
(11)
Poiché deve essere rispettata la congruenza sullo spostamento all'interfaccia tra gli strati, ovvero lo spostamento in sommità ad uno strato deve essere uguale allo spostamento sul fondo di quello immediatamente sopra, se ne deduce che:
(12)
Usando la (10), (11) e la (12), ne consegue che
(13)
Il taglio in sommità ed al fondo dell'm-esimo strato è dato da:
(14)
(15)
Poiché fra uno strato e l'altro il taglio deve essere continuo si ha
(16)
ovvero
(17)
Sommando la (13) alla (17) e sottraendo la (17) alla (13) si ottiene
(18)
(19)
dove 
rappresenta il coefficiente di impedenza complesso al contorno tra gli strati m ed m+1, ed è dato dalla seguente espressione:
(20)
Poiché in superficie il taglio è nullo,
si deduce che E1 = F1.
Le equazioni (18) e (19) possono essere successivamente applicate agli strati successivi da 2 ad m. La funzione di trasferimento Amn che lega gli spostamenti in sommità degli strati m ed n è definita dalla seguente espressione:
(21)
Amn rappresenta la funzione di trasferimento, ovvero la funzione che mette in relazione il modulo della deformazione tra i punti m e n.
In pratica lo stato deformativo di una stratigrafia rimane definito una volta nota la deformazione di un suo qualsiasi punto. Inoltre, poiché la velocità e l'accelerazione sono legati allo spostamento,
(22)
La funzione di trasferimento Amn può essere espressa anche in funzione delle velocità e dell'accelerazione al tetto degli strati n ed m:
(23)
La deformazione tangenziale rimane definita alla profondità z e al tempo t dalla relazione:
(24)
E la corrispondente tensione tangenziale, dalla seguente espressione:
(25)
Ai fini di una corretta interpretazione del problema della risposta sismica locale, risulta utile riprodurre la rappresentazione schematica di Figura 2 in cui è riportata la terminologia utilizzata per lo studio del moto sismico di un deposito che poggia su un basamento roccioso.
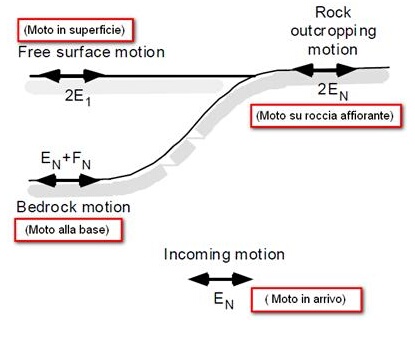
Le onde di taglio si propagano verticalmente attraverso il bedrock con ampiezza pari ad EN; al tetto del bedrock, sotto il deposito degli strati di terreno, il moto ha un'ampiezza pari a EN+FN. Sulla roccia affiorante, poiché le tensioni tangenziali sono nulle (EN = FN), il moto avrà ampiezza pari a 2EN. La funzione di trasferimento dal bedrock al bedrock-affiorante è la seguente:
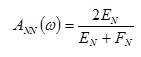(26)
A è non lineare poiché G è funzione di γ. Nella procedura di calcolo infatti, da una stima iniziale del modulo di deformazione al taglio, si ottiene la tensione ipotizzando un legame lineare, per poi ottenere un nuovo valore di γ. Grazie a questo valore aggiornato si valuta un nuovo modulo G così da ripetere la procedura fino a quando la differenza tra la deformazione aggiornata e quella ottenuta dalla precedente iterazione viene ritenuta accettabile.
© Geostru