L’avvio dell’analisi di risposta sismica bidimensionale è collocato nel menu Analisi. Il comando Analisi risposta simica visualizza la finestra in cui vanno inseriti i parametri dell’analisi e gli accelerogrammi.
Input sisma
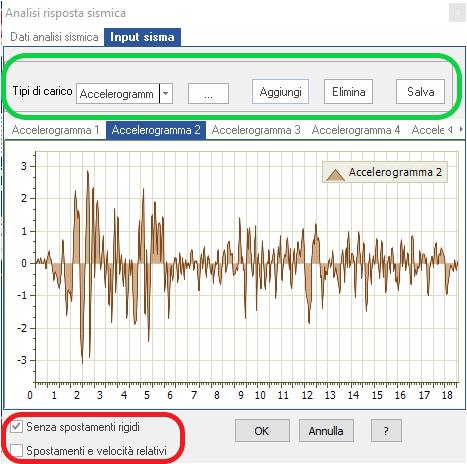
Nalla scheda Input sisma si possono aggiungere fino ad un massimo di 10 accelerogrammi. La selezione del file TXT dell’accelerogramma si esegue dal pulsante … presente vicino a Tipo di carico nel riquadro verde. Nella stessa scheda è possibile scegliere due opzioni di analisi:
a) Senza spostamenti rigidi
b) Spostamenti e velocità relativi
L’opzione (a) non considera, nell’analisi dinamica, lo spostamento assoluto rigido del sistema. Generalmente questa opzione va selezionata in quanto gli spostamenti rigidi non comportano sforzi supplementari.
Selezionando l’opzione (b), a fine calcolo, viene restituito per ogni nodo lo spostamento relativo, diversamente lo spostamento restituito è quello assoluto.
L’importazione degli accelerogrammi è gestita dalla finestra sotto raffigurata e vien richiamata dal click sul pulsante … presente vicino a Tipo di carico.
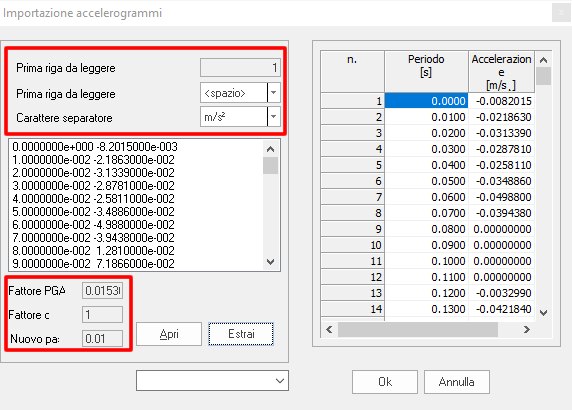
La finestra di selezione del file TXT consente di scegliere la prima riga della registrazione, il campo separatore del periodo e dell’accelerazione e l’unità di misura dell’accelerazione registrata.
Il comando Estrai acquisisce la registrazione visualizzata in anteprima. Nel riquadro rosso può essere variata l’accelerazione di picco PGA, considerare un fattore di scalatura e impostare un nuovo passo di scansione dell’accelerogramma.
Quest’ultimo è impostato di default sul passo dell’accelerogramma importato.
Dati analisi sismica
Il software RSL III 2D consente di effettuare tre tipi di analisi:
▪Analisi lineare a smorzamento variabile
▪Analisi lineare a smorzamento costante
▪Analisi non lineare equivalente
Dal punto di vista teorico, l'analisi dinamica per un numero finito di nodi viene eseguita risolvendo un sistema di equazioni del tipo:
![]()
dove
[M] = matrice delle masse
[C] = matrice degli smorzatori
[K] = matrice delle rigidezze
R = vettore dei carichi noti e pari a [M]ag con ag accelerogramma di input.
u è il vettore degli spostamenti relativi.
La risoluzione del sistema avviene nel dominio del tempo secondo il criterio di Newmark: esso consiste in una serie di integrazioni successive, per ogni passo Δt, che consente di determinare la velocità e, quindi, lo spostamento relativo u. Nell'applicazione del metodo di Newton sono richiesti alcuni parametri d'integrazione.
Parametri integrazione
Parametri di integrazione per la risoluzione del sistema (riquadro giallo in figura sottostante).
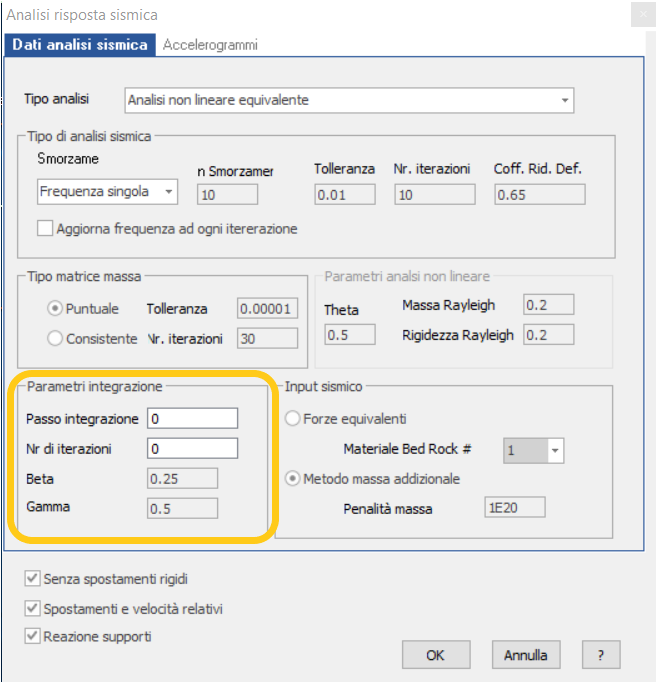
Il passo integrazione riguarda la scansione dell’accelerogramma considerato nel calcolo. Generalmente è pari al passo della registrazione, diversamente, in questa casella è possibile definirne uno personalizzato.
Nr. step, rappresentano il numero di intervalli, funzione del passo d'integrazione, in cui viene suddiviso l'accelerogramma durante l'integrazione.
Beta e Gamma: sono due parametri del metodo di integrazione di Newmark che generalmente hanno valore, rispettivamente, di 0.25 e 0.5.
Ricordiamo che il metodo qui considerato permette, tramite integrazioni successive, di passare dall’accelerazione alla velocità e, quindi, allo spostamento.
Lo smorzamento del terreno è messo in conto attraverso la matrice [C]. Per ogni elemento i in cui è suddiviso il dominio, Ci è calcolata secondo il criterio di Rayleigh, che è correlato con la massa e la rigidezza:
Ci=α∙Mi+β∙Ki
Dove α e β sono due coefficienti chiamati, rispettivamente, Rayleigh Mass e Rayleigh Stiffness, mentre Mi e Ki sono la massa e la rigidezza del singolo elemento. Usando questa formulazione si può rendere lo smorzamento λ (o damping ratio) dipendente dalla frequenza circolare secondo la seguente relazione:
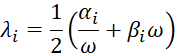
dove α e β per l'elemento i-esimo sono calcolati come segue:
![]()
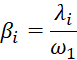
con ω1 la frequenza principale corrispondente al primo modo di vibrazione.
Analisi lineare a smorzamento costante (in rosso nella figura sottostante): il software esegue il calcolo usando la matrice di smorzamento consistente di Rayleigh con α e β costanti per tutti i nodi e pari ai valori indicati in Rayleigh Mass e Rayleigh Stiffness.
Theta è un parametro di integrazione posto, generalmente, pari a 0,5
Analisi lineare a smorzamento variabile: il software esegue il calcolo usando come parametri dello smorzamento quelli definiti nella griglia dei materiali.
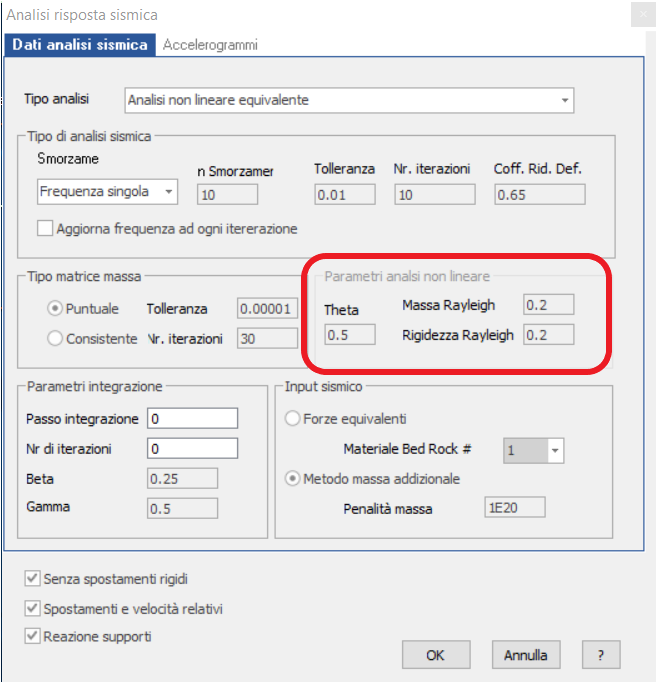
Analisi non lineare equivalente (riquadro verde nell’immagine seguente).
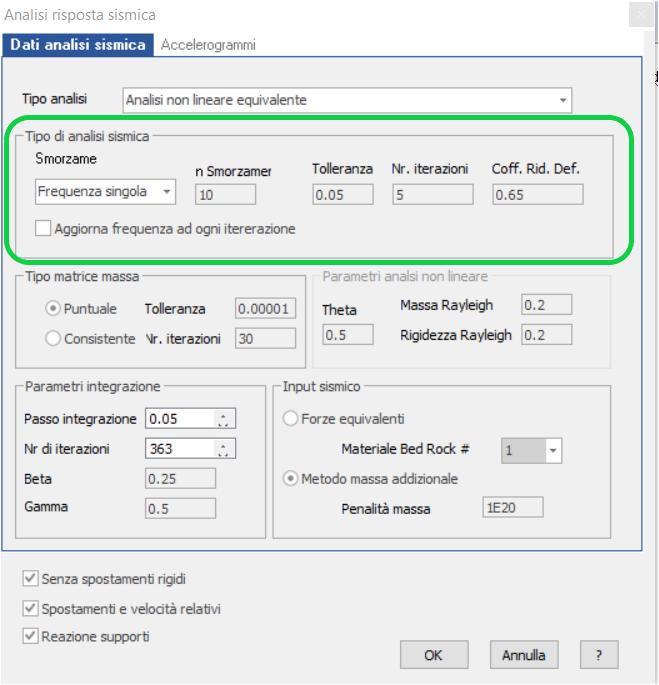
In questo caso il programma esegue una sequenza di analisi lineari in cui i parametri di rigidezza e smorzamento vengono aggiornati iterativamente fino al raggiungimento di un fattore di convergenza. Il calcolo inizia con i valori iniziali di G e D inseriti nella finestra dei materiali e viene determinata la deformazione a taglio collegata al valore dello spostamento u. In ogni iterazione i valori di D e G/Gmax vengono aggiornati in funzione del livello di deformazione efficace raggiunto e il calcolo si ferma quando la differenza dei valori di G e D tra un'iterazione e la successiva è inferiore al livello di tolleranza fissato dall'utente.
Per questa tipologia di analisi si può scegliere di aggiornare anche la frequenza circolare ω ad ogni iterazione. Questo implica che il calcolo dei coefficienti di Rayleigh α e β nella matrice di smorzamento C sono aggiornati ad ogni iterazione per ogni elemento in funzione della frequenza principale ω1, nel caso di Frequenza singola, o di ω1 e ω2 nel caso di Frequenza doppia. Per ciascun elemento, in caso di Frequenza doppia, le espressioni di α e β sono:
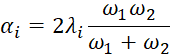
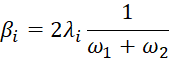
con ω1 frequenza principale e ω2 = nDamp x ω1 , con nDamp generalmente posto pari a 10. In sostanza per ogni iterazione viene calcolata la deformazione di taglio media per ciascun elemento e viene consultata la curva di smorzamento per aggiornare il valore corretto dello smorzamento.
La Tolleranza definisce lo scarto tra i valori di �, G e D, trovati tra un’iterazione e la successiva, che determina la fine del calcolo iterativo.
Il Nr. Iterazioni stabilisce quante iterazioni devono essere eseguite dal programma: un numero elevato di iterazioni (>10) comporta un inutile aggravio dei tempi di calcolo.
Coeff. Rid. Def. È un coefficiente che riduce la deformazione massima, il suo valore, usualmente viene posto pari a 0,65. Esso si calcola dalla seguente espressione: γeff/γmax = (M-1)/10
Altri parametri dell’analisi non lineare equivalente riguardano l’analisi modale ad elementi finiti in cui va definita la matrice di massa (riquadro blu):
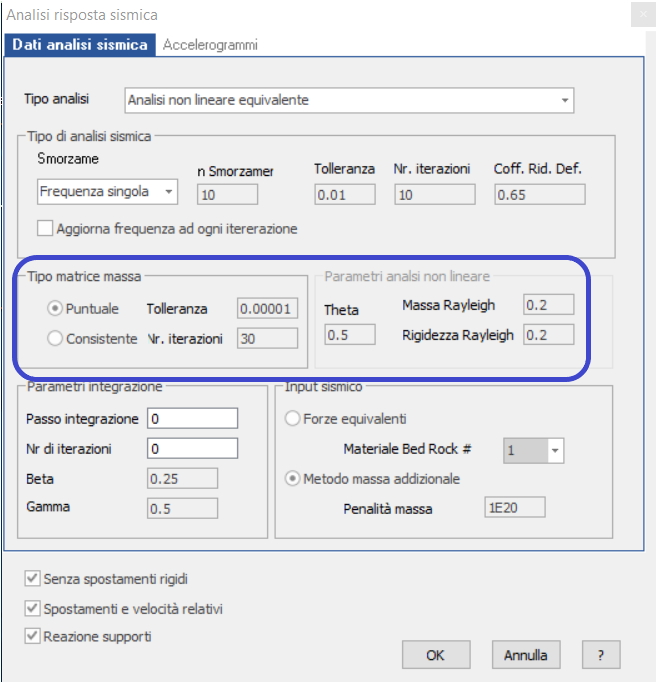
Massa puntuale (“lumped”): la massa viene considerata concentrata nei nodi.
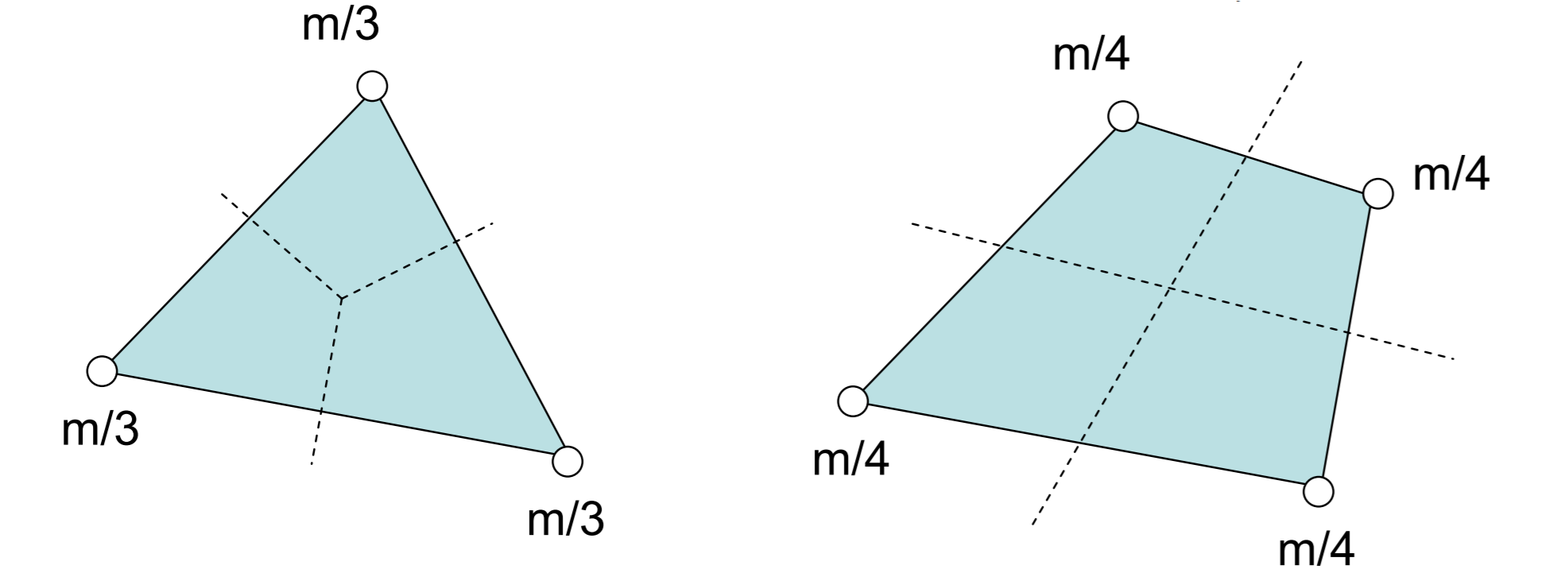
In questo caso la struttura della matrice di massa è diagonale e comporta notevoli vantaggi per la minore occupazione di memoria e la consistente riduzione dei tempi di calcolo. Di solito, questa assunzione, non comporta grossi errori e quindi è preferibile.
Massa consistente (“consistent”): la massa è distribuita e la corrispondente matrice è sostanzialmente piena e simmetrica. Questa assunzione produce errori minori in valore assoluto, ma comporta un aggravio nei tempi di calcolo.
Parametri analisi modale: per l’analisi modale occorre fissare un fattore di Tolleranza, che stabilisce quando si deve fermare il calcolo, e un Nr. di iterazioni. Se il calcolo raggiunge il numero di iterazioni impostato, esso si ferma anche se non è stata raggiunta la tolleranza desiderata. L'analisi modale va eseguita per tutti i nodi del dominio, quindi non è effettuata dal software quando sono presenti nodi monitorizzati.
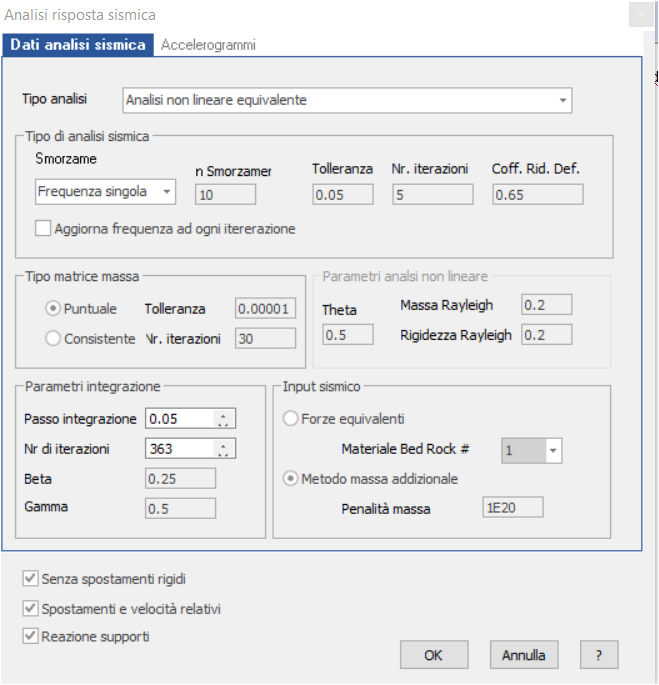
Input sismico
Nell'esecuzione del calcolo di RSL è possibile scegliere due differenti metodologie: Forze equivalenti e Metodo massa addizionale.
Con il primo approccio l'input sismico è definito in termini di forze nodali equivalenti (o forze sismiche effettive), che sono proporzionali alla velocità dell'onda incidente e sono applicate nella direzione orizzontale lungo la base del dominio definito dal modello. Questo tipo di input sismico (outcrop input) viene considerato come una una forza di taglio temporale:
![]()
Dove ρ è la densità del bedrock, Vs rappresenta la velocità delle onde S nel bedrock, v(t) rappresenta la velocità del sisma e A rappresenta il contributo areale associato al nodo caricato.
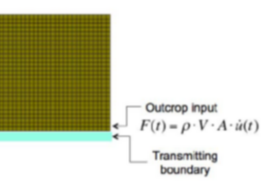
Input sismico approccio Forze equivalenti
Tali forze sono calcolate in automatico dal software e sono applicate nei nodi del dominio a contatto con il bedrock, quindi il vantaggio di questo metodo è, appunto, quello di non dover modellare lo strato del bedrock ma bisogna solo scegliere il materiale di cui è costituito. Selezionando questo metodo le condizioni al contorno, nella Fase 1 (Stage 1) sono rappresentate da molle sia in orizzontale (H) che in verticale (V) per tutti i nodi di controno del dominio. Nella Fase 2 (Stage 2) il software calcola in automatico le reazioni delle molle per tutti i contorni del dominio.
Nota 1: La velocità viene acquista dall'accelerazione del terremoto ipotizzando condizioni iniziali nulle, quindi le serie temporali della velocità sono determinate come:
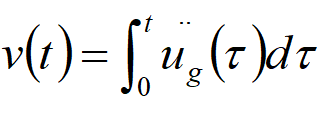
dove ug(τ) è l'accelerazione registrata (outcrop acceleration)
Nota 2: Quando
©GeoStru