The forces acting on the mass that slides include the weight of soil, W, seismic horizontal and vertical pseudo static forces KxW e KYW, the horizontal and vertical forces X and Y applied externally to the slope profile, the resultant of the total normal and shear stresses σ and τ acting on the potential sliding surface.
The total normal stress can include an excess of the pore pressure u that must be specified with the introduction of the parameters of effective force.
In practice, this method can be considered as an extension of the method of the circle of friction for homogeneous sections previously described by Taylor.
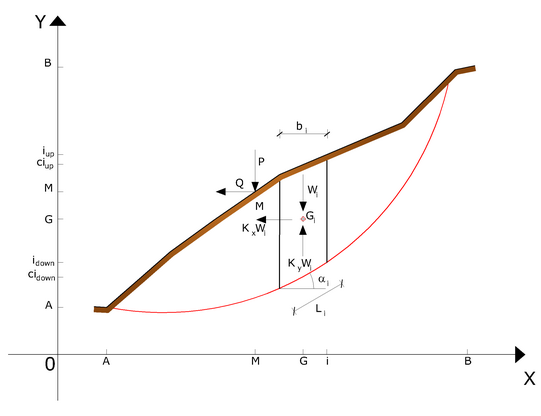
Representation on the Cartesian plane of the block and of the forces acting on the i-the slice
In accordance with Mohr-Coulomb theory in terms of effective stress, the shear stress acting on the base of the i-the slice is given by:
![]()
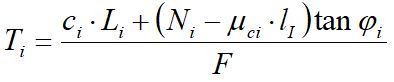
where:
F = safety factor;
ci = the effective cohesion (or total) at the the base of the i-the slice;
φi= the effective friction angle (= 0 with the total cohesion) at the the base of the i-the slice;
Li = the length of the base of the i-the slice;
μci =the pore pressure at the center of the base of the i-the slice.
The equilibrium is obtained by equating to zero the sum of the horizontal forces, the sum of the vertical forces and the sum of the moments compared to the origin.
Is adopted the following assumption on the variation of the normal stress acting on the potential sliding surface:
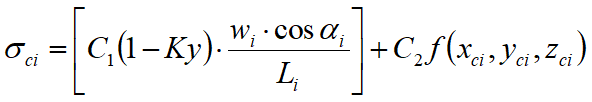
in which the first term of the equation includes the expression:
Wi cos αi / Li = total value of the normal stress associated with the ordinary method of the slices.
The second term of the equation includes the function:
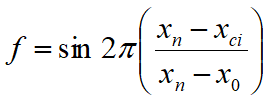
Where x0 and xn are respectively the abscissa of the first and the last point of the sliding surface, while xci represents the abscissa of the midpoint of the base of the i-the slice.
A sensitive part of weight reduction associated with a vertical acceleration of the ground Ky g can be transmitted directly to the base and this is included in the factor (1 - Ky).
The total normal stress at the base of a slice is given by:
![]()
The solution of the equations of equilibrium is obtained by solving a linear system of three equations obtained by multiplying the equilibrium equations for the safety factor F, substituting the expression of Ni and multiplying each term of the cohesion by an arbitrary factor C3.
It is assumed a linear relation between the coefficient, determined using Cramer's rule, and the safety factor F. The corrected value of F can be obtained from the linear interpolation formula:
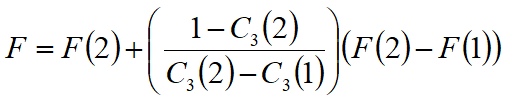
where the numbers in parentheses (1) and (2) indicate initial and subsequent values of the parameters F and C3.
Any pair of values of the safety factor in the close to a physically reasonable estimate can be used to initiate an iterative solution.
The required number of iterations depends on the initial estimate and the desired accuracy of the solution, normally, the process converges rapidly.
© GeoStru