The method of Sarma is a simple, but accurate method for the analysis of slope stability, which allows determining the horizontal seismic acceleration required so that the mass of soil, delimited by the sliding surface and by the topographic profile, reaches the limit equilibrium state (critical acceleration Kc) and, at the same time, allows obtaining the usual safety factor obtained as for the other most common geotechnical methods.
It is a method based on the principle of limit equilibrium of the slices, therefore, is considered the equilibrium of a potential sliding soil mass divided into n vertical slices of a thickness sufficiently small to be considered eligible in the assumption that the normal stress Ni acts in the midpoint of the base of the slice.
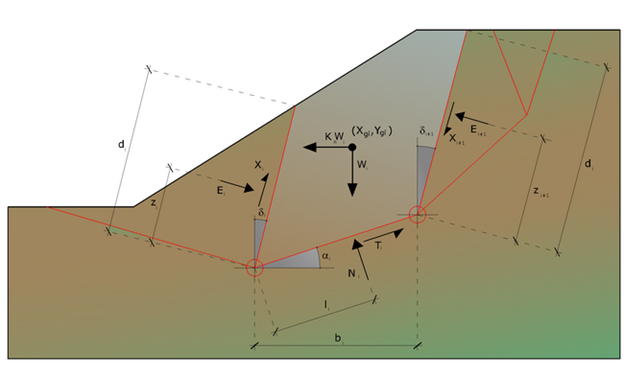
Actions on the i-the slice according to Sarma
The equations to be taken into consideration are:
•The equation of equilibrium to the horizontal translation of the single slice;
•The equation of equilibrium to the vertical translation of the single slice;
•The equation of equilibrium of moments.
Equilibrium conditions to horizontal and vertical translation:
Ni cos αi + Ti sin αi = Wi - ΔXi
Ti cos αi - Ni sin αi = KWi +ΔEi
It is also assumed that in the absence of external forces on the free surface of mass occurs:
ΣΔEi = 0
ΣΔXi = 0
where Ei and Xi represent, respectively, the horizontal and vertical forces on the face of the generic i slice.
The equilibrium equation of moments is written choosing as a reference point the center of gravity of the entire mass; so that, after performing a series of trigonometric and algebraic positions and transformations, in Sarma's method the solution of the problem passes through the resolution of two equations:
![]()
![]()
But the solution approach, in this case, is completely inverted: the problem in fact makes it necessary to find a value of K (seismic acceleration) corresponding to a given safety factor; and in particular, find the acceleration value K corresponding to the safety factor F = 1, that is, the critical acceleration.
Therefore:
K = Kc critical acceleration if F = 1
F = Fs safety factor in static conditions if K = 0
The second part of the problem of Sarma's method is to find a distribution of internal forces Xi and Ei such as to verify the equilibrium of the slice and the global equilibrium of the whole body, without breach of the failure criterion.
It has been found that an acceptable solution of the problem can be achieved by assuming the following distribution for the Xi forces:
![]()
where Qi is a known function, in which are taken into consideration the average geotechnical parameters on the i-the face of the slice i, and λ represents an unknown.
The complete solution of the problem is obtained therefore, after a few iterations, with the values of Kc, l and F, that allow to obtain even the distribution of interslice forces.
© GeoStru