The method is based on the following assumptions:
The interslice forces along the division surfaces of the individual slices are oriented parallel to one another and inclined compared to the horizontal by an angle q, all moments are null Mi =0 i=1…..n
Basically, the method satisfies all the statics equations and is equivalent to the method of Morgenstern and Price when the function f(x) = 1.
Imposing the equilibrium of moments from the center of the arc described by the sliding surface:
|
(1) |
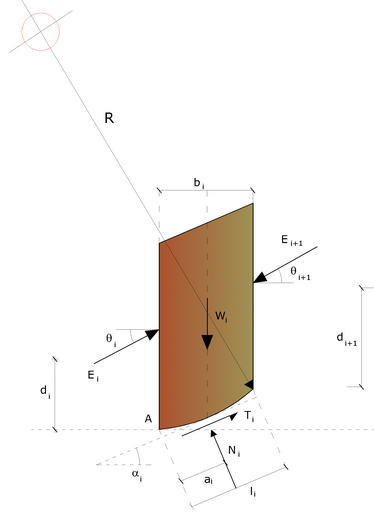
Actions on the i-the slice according to Spencer
where:
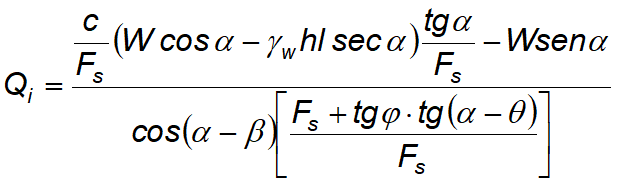
interaction force between the slices;
R = radius of the arc of the circle;
θ = angle of inclination of the force Qi from the horizontal.
Imposing the equilibrium of horizontal and vertical forces we have respectively:
|
(2) |
With the assumption of Qi forces parallel to each other, we can also write:
![]()
The method proposes to calculate two safety factors: the first (Fsm) obtainable from 1), related to the equilibrium of moments, the second (Fsf) obtainable from 2) related to the equilibrium of forces. In practice, we proceed by solving 1) and 2) for a given range of values of the angle θ, considering as a unique value of the safety factor that for which
Fsm = Fsf.
© GeoStru