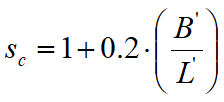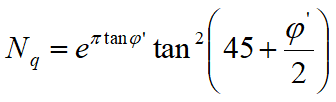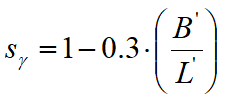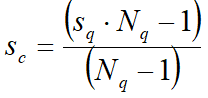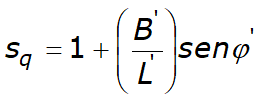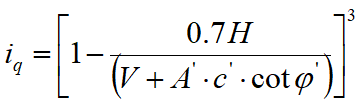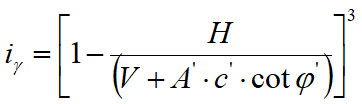Brinch - Hansen (EC 7 – EC 8)
In order for the foundation of a wall to safely sustain the design load in regard to general failure, the following inequality must be satisfied:
![]()
where:
Vd is the design load, normal to the footing, including the weight of the wall;
Rd is the design limit load of the foundation for normal loads, also taking into account eccentric and inclined loads.
In the analytical evaluation of the design limit load Rd must be considered situations for short and long term in fine-grained soils. The design limit load in undrained conditions is calculated as:
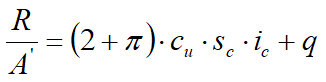
where:
|
Design effective foundation area. When eccentric loads are involved, use the reduced area with the resultant load applied at the center for the area. |
cu |
Undrained cohesion |
q |
Total lithostatic pressure to the substrate |
sc |
Form factor |
|
Form factor for rectangular foundations |
|
Form factor for square or circular foundations. |
|
Correction factor for the inclination of the load due to a load H. |
Design limit load in drained conditions is calculated as follows:

where:
|
|
|
represent the bearing capacity factors and are functions of the internal friction angle.
The form factors are defined by the following relations and were determined in part analytically in part by empirical procedures.
|
for a square or circular shape |
|
for rectangular shape |
|
for square or circular shape
|
|
for rectangular, square or circular shape |
|
for rectangular shape |
Resultant inclination factors due to a horizontal load H parallel to B'
|
|
|
If H forms an angle θ with the direction of L’ :
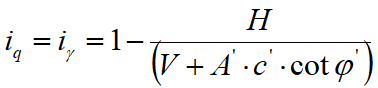

In addition to the correction factors mentioned above are also considered the ones complementary to the depth of the bearing surface and of the ground level (Hansen).
© GeoStru